Learning Resources
Activity
Section 01 Complex Numbers
For exercises 1 to 4, write the number as a pure imaginary number in the form bi and simplify.
1. ![]() 2.
2. ![]() 3.
3. ![]() 4.
4. ![]()
For exercises 5 to 10, perform the indicated operations and leave all i number answers in simplest terms.
5. ![]() 6. 2i x 3i 7. 8i - 15i 8. i 11 x i 12
6. 2i x 3i 7. 8i - 15i 8. i 11 x i 12
9. i 6 + i 20 10. 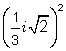
11. Evaluate 2x3 - 4x2 + 6x - 3 for x = ![]()
For exercises 12 to 17 perform the indicated operations and express your answer in simplest terms.
12. (10 - 6i) - (7 - 3i) 13. (4 + i ) - (3 + 2i) - (2 + 3i)
14. 2(5 + 3i) - (3 + i)(1 - i) 15. (5 + 2i)(1 - 3i)(2 + i)
16. (1 - i)3 17. 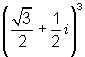
18. Evaluate x2 + x + 1 for x = ![]()
19. Show that 3 + 2i and 3 - 2i are roots of the equation x2 - 6x = - 13 .
20. Show that ![]() and
and ![]() are zeros of the function f(x) = x2 - 4x + 9 .
are zeros of the function f(x) = x2 - 4x + 9 .
Section 02 Polynomial Equations
Factor completely over the system of real numbers the polynomials in exercises 1 - 9 .
1. 32x3 - 48x2 2. 3x2 - 27 3. x4 - 16
4. 3x2 - 24x + 48 5. x2 - 9x + 18 6. 2n2 - n - 3
7. 3n2 + 2nr - 3n - 2nr 8. 9x2 + 26x + 16 9. 4x2 - 7
Find all roots, real or imaginary, of the equations in exercises 10 - 19
10. 3x2 = 5x 11. x2 - 3x = 40
12. 2x3 - 238x = 0 13. 5x2 - 14x - 3 = 0
14. (x + 6)(x - 4) = 24 15. (x + 4)2 = 19(x + 4)
16. x3 + 5x2 - x - 5 = 0 17. 51x2 + x - 92 = 0
18. x4 - 41x2 + 400 = 0 19. ![]()
20. Find the quotient and remainder on dividing 2x3 - 3x2 + 5x - 7 by x - 2. Then express 2x3 - 3x2 + 5x - 7 as (x - 2)(Quotient) + Remainder.
21. One of the factors of 6x3 + 13x2 - 4 is x + 2 . Find the other factors.
Find the rational roots of the polynomial equations in exercises 22 - 24 (Hint: Use the rational roots theorem).
22. x3 - 4x2 + x + 6 = 0 23. 2x3 - 5x2 - 14x + 8 = 0 24. 12x3 + x2 - 10x - 3 = 0
Section 03 Graphs
Use your knowledge of the "basic shape" and the relation between the real zeros and the x-intercepts to sketch the graph of each of the following functions. Do not use graphing technology other than as a check of your work.
1. f(x) = 2 2. f(x) = - ( x + ![]() )
)
3. f(x) = ![]() (x - 1) 4. f(x) = -
(x - 1) 4. f(x) = - ![]() (x - 3)(x + 2)
(x - 3)(x + 2)
5. f(x) = (x + ![]() )( x -
)( x - ![]() ) 6. f(x) = x2 - 3x - 4
) 6. f(x) = x2 - 3x - 4
7. f(x) = -(x + ![]() )(x - 1)(x - 3) 8. f(x) = x3 + x2 - 9x - 9
)(x - 1)(x - 3) 8. f(x) = x3 + x2 - 9x - 9
9. f(x) = (x + 3)2(x - 1)(x + 2) 10. f(x) = - x4 + 26x2 - 25
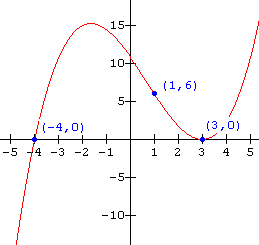
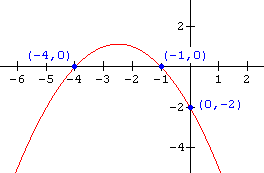
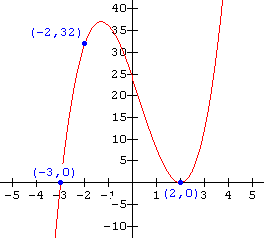
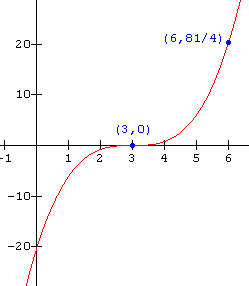
Find the function for each of the graphs shown below:
11. 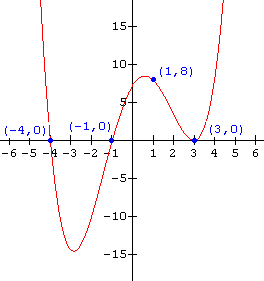 12.
12. 
13. 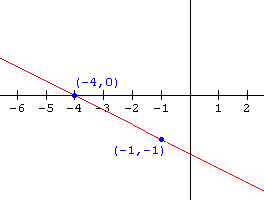 14.
14. 
15. 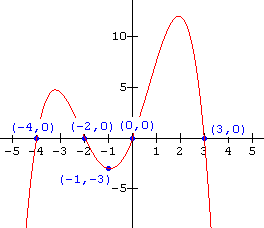 16.
16. 
Section 04 Radical Equations
Solve each of the following equations:
1. ![]() 2.
2. ![]()
3. ![]() 4.
4. ![]()
5. ![]() 6.
6. ![]()
7. ![]() 8.
8. ![]()
Test Yourself
1. Given the polynomial 3x2 - 4x3 + 2x - x4 + 5
(a) What type of polynomial is it?
(b) What is the degree?
(c) What is the leading coefficient?
2. Simplify:
(a) i 15 x i 17 (b) (2 + 5i) + (9 - 3i) - (6 - 2i) (c) (3 - i![]() )(2 + 3i
)(2 + 3i![]() )
)
3. Verify that ![]() is a zero of the function f(x) = 3x2 - 4x + 2 .
is a zero of the function f(x) = 3x2 - 4x + 2 .
4. Find all the real roots of each of the following equations:
(a) ![]() (b) 4x2 + 12x + 9 = 0
(b) 4x2 + 12x + 9 = 0
(c) 8x2 - 22x + 15 = 0 (d) 36x4 - 25x2 + 4 = 0
(e) x3 + 4x2 - 9x - 36 = 0 (f) ![]()
(g) ![]() (h) 10x3 - 17x2 - 7x + 2 = 0
(h) 10x3 - 17x2 - 7x + 2 = 0
5. What is the remainder when 2x15 - 3x8 + 2x2 - 5 is divided by x + 1 ?
6. Sketch the graph of each of the following:
(a) f(x) = x(x + 3)(x - 2) (b) f(x) = -(x - 3)(x - 4)(x + 2)2
7. Find the function that describes each of the following graphs:
(a) 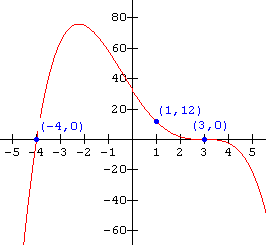 (b)
(b)