Learning Resources
Lesson
Defining Complex Numbers
We have worked with two number systems, the system of real numbers and the system of pure imaginary numbers or i - numbers. We will now define another set of numbers that are formed by adding together a real number and an i - number. This set of numbers is called the complex numbers.
Definition: Every number of the form a + bi , where a and b are real numbers, is called a complex number.
Note that since a = a + 0i , it follows that every real number is also a complex number. Similarly, since bi = 0 + bi , it follows that every pure imaginary number is also a complex number. Consequently, the set of real numbers and the set of i - numbers are contained in the set of complex numbers.
For a given complex number a + bi , it is customary to call a the real part and bi the pure imaginary part of the number. Two complex numbers are equal if and only if their real parts are equal and their pure imaginary parts are equal.
Some examples of complex numbers are given below:
4 + 3i ; 
; 
; 5 ( because it is 5 + 0i ); 3i (because it is 0 + 3i )
You may think that complex numbers have no application in the real world, but that is not the case. For a discussion of the origin of complex numbers and an example of their application to real world problems click here.
Now turn to a discussion of the operations of addition and subtraction (page 2 of this lesson) and multiplication (page 3 of this lesson) of complex numbers.
Adding and Subtracting Complex Numbers
We add two complex numbers by adding their real parts together and then adding their imaginary parts together.
Definition: (a + bi ) + (c + di ) = (a + c) + (b + d)i
Subtraction can be defined in a similar manner, viz. subtract the real parts and then subtract the imaginary parts.
Definition: (a + bi ) - (c + di ) = (a - c) + (b - d)i
The examples below illustrate how to apply this definition.
(- 8 + 4i ) + ( 3 + 5i ) = (-8 + 3) + (4 + 5)i = - 5 + 9i
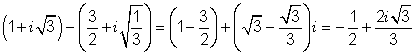
Multiplying Complex Numbers
We want multiplication of complex numbers to satisfy the usual rules of arithmetic and algebra. This includes the use of the distributive property that you applied to binomial expressions that represented real numbers (or the use of the memory device, FOIL). The way that FOIL would be applied is shown in the following example:
F O I L
(2 + 5i )(3 - 4i ) = (2 x 3) + (2 x - 4i ) + (5i x 3) +(5i x - 4i )
= 6 - 8i + 15i - 20i 2
= (6 + 20) + (- 8 + 15 )i
= 26 + 7i
If you were to apply the same technique to multiplying the numbers a + bi and c + di it would lead to the general definition of multiplication of complex numbers as follows:
Definition: (a + bi )(c + di ) = (ac - bd) + (ad + bc)i
Most students find it just as easy to multiply using the distributive property (or FOIL) as memorizing the definition and applying it. That decision is left to you. The following examples are done both ways (using FOIL and applying the definition) for comparison purposes.
Example 1
F O I L
(2 + 3i )(2 - 3i ) = 4 - 6i + 6i - 9i 2
= 13
ac bd ad bc
(2 + 3i )(2 - 3i ) = (4 - (-9)) + (- 6 + 6)i
= 13
Notice in the above example that the imaginary part "disappeared". Notice also the relation between the two numbers, if one is represented as p + qi , the other is p - qi . Complex numbers related this way are called complex conjugates of each other. The product of two complex conjugates is always a real number.
Example 2
F O I L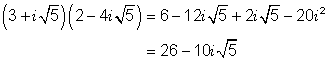
ac bd ad bc
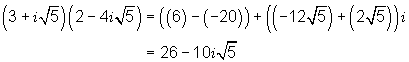
Example 3
F O I L
(5 - i )(6 + 2i )(3 + 3i ) = (30 + 10i - 6i - 2i 2)(3 + 3i )
= (32 + 4i )(3 + 3i )
F O I L
= 96 + 96i + 12i + 12i 2
= 84 + 108i
ac bd ad bc
(5 - i )(6 + 2i )(3 + 3i ) = [(30 - (-2)) + (10 + (-6))i ](3 + 3i )
= (32 + 4i )(3 + 3i )
ac bd ad bc
= (96 - 12) + (96 + 12)i
= 84 + 108i
As Roots of Polynomial Equations
A number which makes an equation true is referred to as a root of the equation. In the next section of this unit we will explore how to find the roots of polynomial equations of degree four or less. There we will discover that the number of roots of a polynomial equation corresponds to the degree of the polynomial.
In this lesson we limit our discussion to verifying whether a given number is a root of a given equation. To do this we simply substitute the number into the equation and see if it makes it true. This idea is shown in the following example.
Example 1
Which, if any, of the following numbers is a root of the equation x2 - 2x = - 5 ?
(a) 2 + i (b) 1 + 2i (c) 
Solution
(a)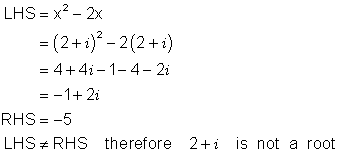 
(b)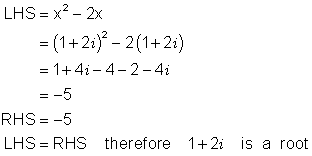 
(c)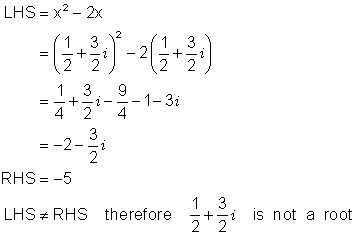 
Closely associated with the root of an equation is the zero of the corresponding function. A zero of a function is the domain value which makes the range value of the function equal to zero. Again, we will discuss this in the next section. In this lesson we limit our discussion to verifying whether a given number is a zero of a given function. To do this we simply substitute the number into the equation and see if it returns a range value of zero. This idea is shown in the following examples.
Example 2
Which, if any, of the following numbers is a zero of the function f(x) = x3 + 5x2 + 11x + 15 ?
(a) 1 + 2i (b) 1 - 2i (c) -1 - 2i
Solution
(a)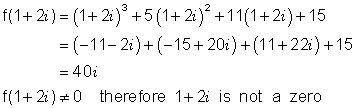 
(b)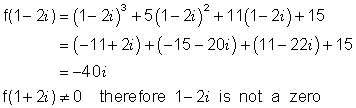 
Note that 1 + 2i and 1 - 2i are complex conjugates. If one had been a zero of the function than so would the other. We will discuss this relation in more detail in the next section of this unit.
(c)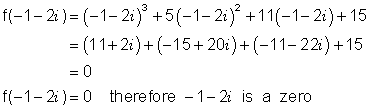 
Now verify for yourself that the conjugate, which is -1 + 2i , is also a zero of the function.
Activity
Print off a copy of this page and add it to your Math 3103 binder. Then answer the questions in your binder.
For exercises 1 to 10, perform the indicated operations and express your answer in simplest terms.
1. (7 - 8i ) + ( - 5 - i ) 2. 
3. 
4. 
5. 
6. (4 - 7i )(3 - 2i )
7. 
8. 
9. 
10. 
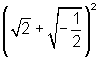
11. Which, if any, of the following numbers are zeros of the function f(x) = x3 - 6x2 + 21x - 26 ?
(a) 2 - 3i (b) 2 + 3i (c) 3i (d) 2
12. One root of the equation x2 - 2x = 16 is 1 + 4i . Show that the conjugate of 1 + 4i is also a root of the equation.
Test Yourself
For exercises 1 to 10, perform the indicated operations and express your answer in simplest terms.
1. (5 + 2i ) + ( - 9 - 5i ) 2. - (3 - 2i ) - ( 5 - 5i )
3. 6(2 + i) - 3(3 + 2i ) 4. ( 2 + 7i ) - ( 3 + 4i ) + ( 7 - 6i )
5. 
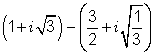6. ( 5 - 2i )(5 + 2i )
7. 
8. ( 13 + 4i )( 12 - 9i )
9. 
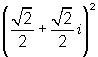10. 
11. (a) Show that 
is a root of the equation x3 = 1. That is, show that is a cube root of 1.
(b) Other than what are the other two cube roots of 1 ?