Learning Resources

Complex Numbers

Defining Complex Numbers

The adjectives imaginary and complex indicate the struggle that took place in the minds of sixteenth-century mathematicians who first dared to use such numbers. As late as 1770, Euler apologized for the frequent use of complex numbers in his algebra book. He wrote:

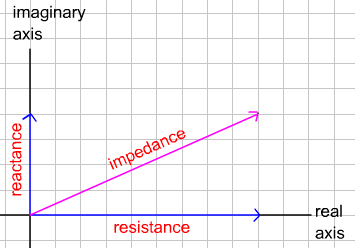
"All such expressions as   (the number i ) , , and so on are impossible or imaginary numbers since they represent roots of negative quantities, and of such numbers we may truly assert that they are neither nothing, nor greater than nothing, nor less than nothing, which necessarily constitutes them imaginary or impossible."

Euler's apology to the contrary, modern scientists and mathematicians have found many situations in the real world that can be described by complex numbers. For example, in physics, when two forces act at right angles to each other, one force can be represented by a real number a, and the other by an imaginary number bi . Then the combined forces (the resultant) may be represented by the number a + bi . 

One application of this concept is to the flow of a current in an electric circuit. Impedance in an electric circuit is a combination of resistance (which is represented by the real part of the complex number) and reactance (which is represented by the imaginary part of the complex number). Each of these is measured in ohms, the symbol for which is W.

Example:

If the resistance of a circuit is 12W and the reactance is 7W , then the impedance can be described by the complex number 12 + 7i  . The value of the impedance is found by taking the absolute value of the complex number, viz.