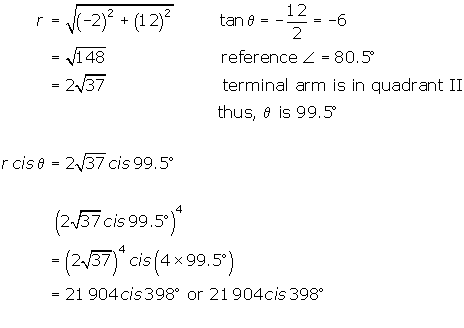Learning Resources
Lesson
You will compare ways to evaluate powers of complex numbers written in rectangular form with evaluation of powers written in polar form. This comparison activity will lead you to the discovery of De Moivre's Theorem.
Powers of complex numbers, you will realize, can involve time consuming calculations. As you saw earlier, patterns are incredibly useful in helping to evaluate complex numbers. Often, converting the complex numbers from one form to another will make the evaluation process easier.
Pairs or small groups are suggested for this Investigation. In fact, it might be best if you work in the same groups used for Investigation 5.
Read the introduction to the Investigation on page 303. Evaluate the three given powers of complex numbers. Recall that squaring a binomial results in a trinomial.
You may verify your final answer to each question before moving on to the Investigation Procedure.
Now, you are to use your knowledge of multiplication of complex numbers in polar form to evaluate powers of complex numbers in polar form. You will investigate the patterns that result between the exponent and the answer. Record each observed pattern.
Carry out the Investigation. Hints and suggestions are offered for various steps, should you require assistance.
Answer the Investigation Questions.
A summary of the Investigation is provided.
Notebook Entry:Record De Moivre's Theorem, and accompany it with an
Activity
C.Y.U. page 306 #'s 19 - 24
When you have completed these questions, ask your on-site teacher to get the solutions for you from the Teacher's Resource Binder and check them against your answers. After you do this, if there is something you had trouble with and still do not understand, contact your on-line teacher for help.
Test Yourself
Simplify each expression.
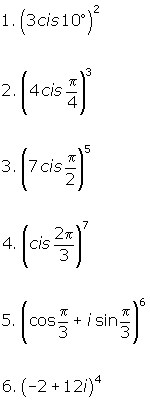
Solutions
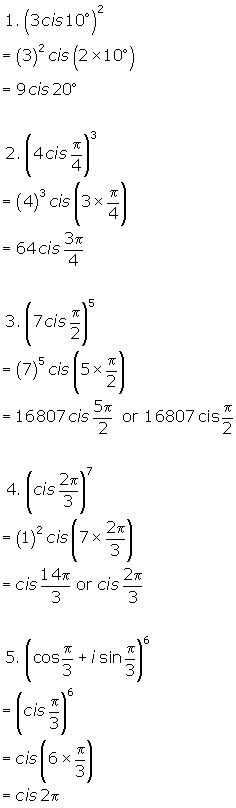
6. First, you must write (-2 + 12i )4 in the form r cis![]() , so you can apply De Moivre's Theorem.
, so you can apply De Moivre's Theorem.