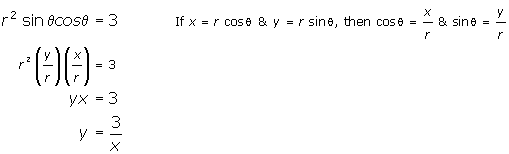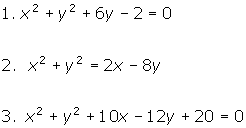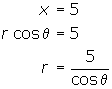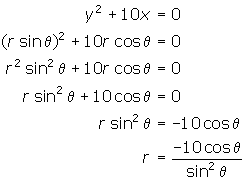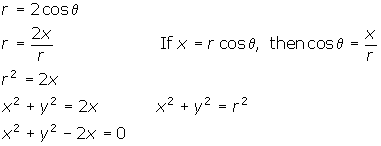Learning Resources
Lesson
In Mathematical Modeling, Book 3, you found the centre and radius of many circles. You saw that the centre and radius are easily identified when the equation for the circle is written in standard form as shown below.
Often, however, equations were presented in the general form:
Before identifying the centre and radius, you learned to convert the equation from general form to standard form by the process of completing the square. A reminder of this process is provided, should you need to refresh your memory.
Before beginning Focus F, change each equation below to the form 
, and graph the resulting circle.
An alternate approach to graphing circles is to change the equation to polar form, then graph it on a polar grid.
Consider the equation 
, the centre and radius of which you previously found by the process of completing the square. This equation, in rectangular form, can be difficult to graph. Changing the equation to polar form, and graphing on a polar grid, will decrease the difficulty.
To understand the process of converting rectangular equations to polar equations, you must understand the following facts.
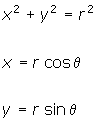
These formulas are substituted into the rectangular equation, as illustrated below.
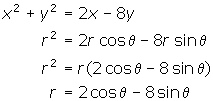
Graph the above polar equation on your TI-83 Plus calculator. The resulting circle should be the same as the one you previously graphed on a rectangular grid.
If you require assistance graphing polar equations using technology, consult page 298 of your text for instructions.
Without the use of polar equations, an equation of the form 
would be a challenge to graph.
However, it can be converted to polar form, and sketched quite easily. The process is as follows.
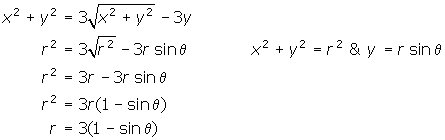
Graph the resulting polar equation on your calculator.
What about changing equations in polar form to rectangular form? The same facts still apply. The key is to realize that you want to get the equation in terms of x and y.
You already saw that x = r cos
and y = r sin. Thus:
The rearrangement of these formulas will prove useful in converting from polar to rectangular equations.
Write the equations below in rectangular form.
-
r = 3sin
-
r 2 sin
cos = 8
Read the Focus as outlined on pages 297 & 298.
A summary of the knowledge you must have to translate between polar and rectangular form is provided.
Answer the Focus Questions, paying particular attention to the notes in the margin.
Activity
Focus Questions page 298 #'s 27 - 29
When you have completed these questions, ask your on-site teacher to get the solutions for you from the Teacher's Resource Binder and check them against your answers. After you do this, if there is something you had trouble with and still do not understand, contact your on-line teacher for help.
Test Yourself
- Write x = 5 in polar form.
- Write
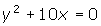in polar form. - Write
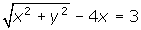in polar form. - Write r = 2cos in rectangular form.
- Write r2 sin cos = 3 in rectangular form.
Solutions
1. Recall: x = r cos.
2. The goal is to get an equation for r in terms of .
3. 
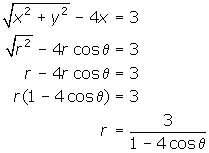
4. The goal is to get an equation in terms x and y.
5. 