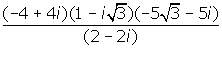Learning Resources
Lesson
Simplify the expression below.
Give this problem an honest attempt, as its complexity will set the stage for the need for polar coordinates. Check your solution.
No doubt, you will agree that this was not an easy calculation to complete. Polar coordinates, the topic of this Focus, can often make expressions like this easier to simplify. This expression will be looked at again in Investigation 4, so don't fret too much if you had a lot of difficulty with its simplification. You will soon learn an alternate, easier approach to the problem.
Before beginning the Focus, you must obtain Blackline Master 5.2.1, on page 536 of the Teacher's Resource Book, from your on-site teacher. Photocopy several copies of the polar paper, as you will need it for various activities.
Polar paper consists of a series of concentric circles, having a common centre, O, called the pole. Visualize that the first circle has a radius of one, and each successive circle has a radius equal to one unit greater than the previous circle. The horizontal ray drawn from the pole to the right is called the polar axis.
The location of a point, P, on polar paper is determined by two parameters:
- the distance
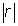from the pole, and - the angular measure,
, between the radius 
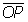and the polar axis.
Points are named in the form (r, ). As with circular functions, if the angle is measured counterclockwise, is positive. If the angle is measured clockwise, is negative.
Although the value for the radius is usually expressed as a positive value, r can be negative as well. A negative value of r will cause a reflection across the pole. In essence, it involves a rotation of 180° or 
radians.
Read the introduction to Focus E on pages 289 of your text.
You must understand that, due to the periodic nature of any function associated with circles, there is more than one set of coordinates to express any point, unlike points graphed on a rectangular coordinate system. An infinite number of coordinates can be used to express a single point.
Complete Example 1 of the Focus on your own polar paper. Follow the given instructions carefully, and check your answers from the diagram in the margin. Two alternative approaches to plotting point D are provided.
Answer the Focus Questions.
Activity
Focus Questions page 290 #'s 1 - 3
C.Y.U. page 291 #4
When you have completed these questions, ask your on-site teacher to get the solutions for you from the Teacher's Resource Binder and check them against your answers. After you do this, if there is something you had trouble with and still do not understand, contact your on-line teacher for help.
Test Yourself
- Graph the point P (2, 50°). Name two other points that would be graphed in the same location as point P.
- Graph Q (5, 120°). Find other coordinates for the same point Q that satisfy each condition below.
(a) r is negative.
(b)
(c)
Solutions
1. To plot point P, follow the instructions below.
- On the polar axis, move to the circle with r = 2.
- Rotate 50° counterclockwise from the polar axis.
- Plot a point on this circle.
Two other points that would be graphed in the same location are (2, 410°) and (2, -310°). Note that these new angles are coterminal with 50°. Thus, there are many possible answers.
2. (a) (-5, 300°) which is found by adding a rotation of 180° to the 120° angle.
(b) (5, -240°) which is found by subtracting 360° from 120°.
(c) (5, 480°) which is found by adding 360° to 120°.
Note: There are many possible solutions to each question.