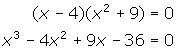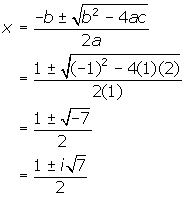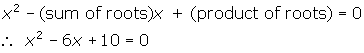Learning Resources

Home »  » Courses » Mathematics » Advanced Mathematics 3207 (delisted) » Unit 05 » Set 01 ILO 05 » Go to Work

Lesson

In Chapter 2, you saw that the degree of a polynomial equation determines the number of roots that exist. The roots may be all real, all imaginary, or a combination of real and imaginary roots may exist. You also learned that if the polynomial equation is of odd degree, then at least one real root exists.

This Focus is designed to examine all the roots of any polynomial equation. Proceed with the steps outlined on page 287 of your text. Hints and suggestions are provided, should you experience difficulty.

• Step A
• Step B
• Step C
• Step D
• Step E
• Step F

Answer the Focus Questions.

An example is provided below.

Note: 

For the next lesson, you will need Blackline Master 5.2.1, found on page 536 of the Teacher's Resource Book. Get this from your on-site teacher before beginning the next section. Photocopy several copies of the polar paper, as you will need it for various activities.

Activity

Focus Questions page 288 #'s 69 - 71

C.Y.U. page 288 #'s 72 & 73

When you have completed these questions, ask your on-site teacher to get the solutions for you from the Teacher's Resource Binder and check them against your answers. After you do this, if there is something you had trouble with and still do not understand, contact your on-line teacher for help.

Test Yourself

1. Solve for x: 4x⁴ - 9 = 0.
2. Solve for x: x² - x + 2 = 0.
3. Given a quadratic equation with integral coefficients. If 15 + 2i is one of its roots, what is the other root?
4. Write a quadratic equation with integral coefficients such that one of its roots is 3 - i.
5. Write a quartic equation with integral coefficients and roots 2i and -5i.
6. Write a cubic equation with integral coefficients and roots 4 and 3i.

Solutions

1.

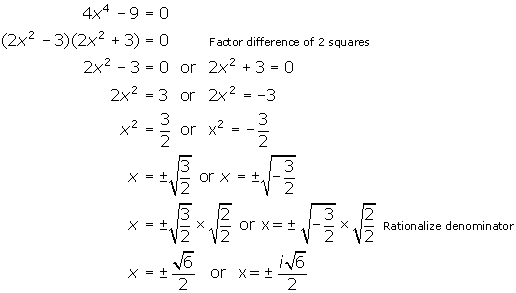
2. This equation is not factorable. Thus, use the quadratic formula.

 

3. The other root is 15 - 2i.

4. The two roots are 3 - i and 3 + i. The sum of these two roots is 6. The product
    of these two roots is (3 - i )(3 + i ) = 9 - i ² = 10. Thus, the related equation is:

 

5.

• The four roots are 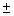2i and 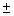5i.
• The sum of 2i and -2i is 0.
• The product of these two roots is -4i ², which is 4.
• Thus, the quadratic equation is x² + 4 = 0.
• The sum of 5i and -5i is also 0.
• The product of these two roots is -25i ², which is 25.
• The related quadratic equation is x² + 25 = 0.
• Thus, the desired quartic equation is: 

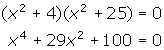
6.

• The three roots are 4 and 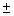3i.
• The sum of the roots 3i and -3i is 0.
• The product of these two roots is -9i², which is 9.
• Thus, the related quadratic equation is x² + 9 = 0.
• Since 4 is a root, (x - 4) is a factor of the cubic equation.
• The desired cubic equation is: