Learning Resources

Investigation 2: Multiplying and Dividing Complex Numbers

Summary

• Multiplying a complex number by the imaginary unit, i, results in a counterclockwise rotation of 90° to obtain the resultant vector.

• Multiplying a complex number by i ² results in a counterclockwise rotation of 180° to obtain the resultant vector.

More generally:

When multiplying a complex number by i ⁿ, where n is an integer, the resultant vector is obtained by rotating the original vector counterclockwise by (90°)n.

• Multiplying a complex number by a constant, c, where c 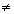0, produces a resultant vector that is a dilatation of the position vector by a factor of c.