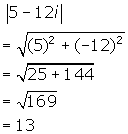Learning Resources
Lesson
Before beginning this Focus, it is important that you understand the concept of imaginary and complex numbers.
A pure imaginary number, you will recall, is in the form bi, where b is a non-zero real number and i is the imaginary unit, where i = ![]() . An example of a pure imaginary number is 6i.
. An example of a pure imaginary number is 6i.
A complex number, however, is the combination of a real number and an imaginary number. It is in the form a + bi, where a and b are real numbers, and i is the imaginary unit. An example of a complex number is 4 + 3i.
However, 6i and 5 are also complex numbers, since each can be written in the form a + bi. We usually write 6i and 5 instead of, respectively, 0 + 6i and 5 + 0i.
The complex number system consists of the real numbers and the imaginary numbers. In essence, a pure imaginary number is a complex number in which
a = 0 and b is any non-zero real number, such as 6i. A real number is a complex number in which b = 0, such as 5. An imaginary number is a complex number in which b ![]() 0.
0.
The table below should serve to clarify each of the above scenarios.
| A complex number a + bi is: | When | Examples |
| a real number | b = 0 | 5 + 0i = 5 |
| an imaginary number | b |
4 + 3i and 0 + 6i |
| a pure imaginary number | a = 0 and b |
0 + 5i = 5i |
This Focus introduces graphing complex numbers on the Argand plane. The key point to ensuring success with graphing on the Argand plane is understanding that the horizontal axis is the real axis and the vertical axis is the imaginary axis.
A complex number a + bi can be expressed as an ordered pair, (a, b). It is this ordered pair that is graphed on the Argand plane. At first glance, the Argand plane looks much like the Cartesian plane used for graphing in the real number system. There are differences however.
Take, for example, the number 2 on the vertical axis. In the Cartesian plane that point is represented by the ordered pair (0, 2). In the Argand plane it is still represented by the ordered pair (0, 2). However, it represents the complex number 0 + 2i, or 2i, since the vertical axis is the imaginary axis.
Similarly, the origin on the Cartesian plane is the ordered pair (0, 0). Whereas, on the Argand plane, although it still corresponds to the point (0, 0), it represents the complex number 0 + 0i, or 0i.
Proceed with the Investigation on pages 277 & 278 of your text. Step A asks that you copy the diagram into your notebook. When doing so, be sure to label each axis. Hints and suggestions are provided for steps C and D. Use them only if you are experiencing difficulty.
Answer the Focus questions.
A summary of the Focus is provided.
Notebook Entry: Record examples of graphed complex numbers to illustrate an Argand diagram. Plot the following complex numbers.
- 5i
- 2 - 3i
- -6 + 4i
- -3
Two examples are provided below.
Activity
Focus Questions pages 278 & 279 #'s 22 - 31
When you have completed these questions, ask your on-site teacher to get the solutions for you from the Teacher's Resource Binder and check them against your answers. After you do this, if there is something you had trouble with and still do not understand, contact your on-line teacher for help.
Test Yourself
The following questions are based on the complex number 5 - 12i.
- What is the coefficient of the real part of the complex number?
- What is the coefficient of the imaginary part of the complex number?
- Write an ordered pair to represent the complex number.
- Find the modulus of the complex number.
Solutions
- 5
- -12
- (5, -12)