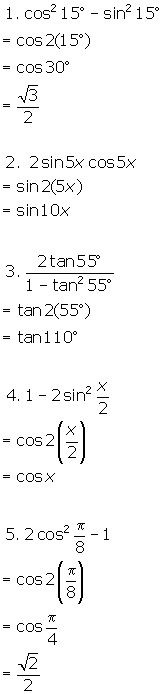Learning Resources
Lesson
In this Focus you will develop the double angle identities for sine, cosine, and tangent. To do so, you will use the compound angle identities developed in Investigation 7B and question #6.
Your goal is to develop formulas for cos2a, sin2a, and tan2a. It will be helpful to substitute (a + a) for the angles.
This Focus is fairly straight forward, as the solution for part (a) is provided. Record the solution in your notebook.
After part (b) of the Focus is completed, verify your solution. Then, answer the questions below before moving to part (c).
- Examine the formula you have developed for cos2a. Using the Pythagorean Identities, rewrite this formula another way.
- Can you rewrite the original formula for cos2a yet another way? Use the Pythagorean Identities to help you.
You will need to refer to question #6 on page 250, to complete part (c) of the Focus. Be sure to identify any restrictions to be placed on the value of a.
Notebook Entry: Record the double angle formulas for sine, cosine and tangent. Remember to record all three formulas for cos2a.
You are not expected to memorize the double angle identities. They will be provided, as required, for testing purposes. You must, however, have a good working knowledge of when and how to apply them.
Note:
You will need graph paper to complete the next Investigation.
Activity
C.Y.U. pages 251& 252 #'s 9 - 14
When you have completed these questions, ask your on-site teacher to get the solutions for you from the Teacher's Resource Binder and check them against your answers. After you do this, if there is something you had trouble with and still do not understand, contact your on-line teacher for help.
Test Yourself
- Find the exact value of cos215° - sin215°.
- Simplify 2sin5x cos5x.
- Simplify
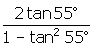 .
. - Simplify
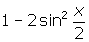 .
. - Find the exact value of
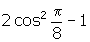 .
.
Solutions