Learning Resources
Lesson
This lesson involves two Investigations, each offering a different strategy for developing the compound angle identities. The approach used in Investigation 7A involves the general rotational matrix, whereas Investigation B makes use of the distance formula. Your on-line teacher may choose to expose you to one, or both, of these methods.
Investigation 7A: Is the Calculator Defective?
Suppose you were asked to evaluate 
, without using the calculator.
This, of course, means the exact value is required for the answer. Presently, you have no exact value at your disposal for .
From your work with the unit circle, you know exact trigonometric values for angles measuring 
.
Can you rewrite 
as the addition or subtraction of two of the above fractions?
You should readily see that 
.
To many of you, it may stand to reason, then, that 
.
Determine the exact value of 
. Once the task is completed, you may verify your solution.
Now, use your calculator to find the value of .
- How does the answer compare to the value of ?
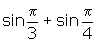- Are they the same or different?
- What conclusion can you make?
After careful consideration has been given to these questions, you may check your responses.
Investigation 7A is best done in small groups. Contact your on-line teacher for instructions on group formation and size.
You will need graph paper for the activity. The first thing you will be required to do is draw a unit circle. Be sure to draw a large one, as you will be adding information to it at later steps of the Investigation. This will ensure your diagram does not become too cluttered. As well, label the origin (1, 0).
Carry out the procedure of the Investigation as outlined on pages 247 & 248 of your text. Hints and suggestions are provided. Use them only if you are experiencing difficulty.
Recall the problem proposed at the beginning of this lesson. You discovered that 
.
Do you know the correct way to evaluate ?
Find the exact value of . Record your answer. Verify your result.
Investigation 7B: The Distance Formula and Compound Angles
This Investigation provides an alternate approach to developing the compound angle formulas. You will develop the compound angle identity for cos(a - b).
It is essential that you review the distance formula before beginning the Investigation.
The first thing you will be required to do in the Investigation is copy a given circle into your notebook. Be sure the circle you draw is large enough so it will not become cluttered as you add information. Proceed with the Investigation as outlined on pages 248 & 249 of your text. Hints and suggestions are available for viewing if you are experiencing difficulty.
Before beginning the Investigation Questions, review the concept of odd and even functions. Answer the following questions in your exercise.
- Is the sine function odd or even? What does this mean?
- Is the cosine function odd or even? What does this mean?
Once completed, you may check your responses.
Investigation Question #2 is a key question, as you are required to develop identities for cos(a + b) and sin(a + b). Hints are provided for parts (a) and (b) of this question, should you require them.
Complete the Investigation questions.
A review of the compound angle identities is provided.
Notebook Entry: Record the compound angle identities.
You are not expected to memorize the compound angle identities. They will be provided, as required, for testing purposes. You must, however, have a good working knowledge of when and how to apply them.
Some examples are provided below.
Activity
C.Y.U. pages 249 & 250 #'s 4 - 8
When you have completed these questions, ask your on-site teacher to get the solutions for you from the Teacher's Resource Binder and check them against your answers. After you do this, if there is something you had trouble with and still do not understand, contact your on-line teacher for help.
Test Yourself
- Give the exact value of sin75° cos15° + cos75° sin15°.
- Calculate the exact value of sin 75°.
- Calculate the exact value of
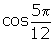. - Prove
.
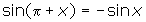Solutions
