Learning Resources
Lesson
To be successful with this Investigation it is essential that you have an understanding of the unit vector. You must understand how to show a unit vector on the unit circle, and successfully perform various transformations.
A unit vector is a vector of length (magnitude) one unit. Specifically, i is a unit vector with its tail at (0, 0) and its head at (1,0). This unit vector can be written as 
.
Similarly, j is a unit vector with its tail at (0, 0) and its head at (0, 1). It can be written as 
.
These two unit vectors will be transformed throughout the Investigation. The length of the unit vector, however, never changes. It is always one unit.
Before beginning Investigation 6, please make note of the following errors in Step E of the Procedure, on page 242. Each bulleted paragraph contains a sentence which refers to the "tail" of a specified unit vector. In each case, replace the word "tail" with the word "head."
The purpose of this Investigation is to develop the general rotational matrix. This is the matrix that will perform a rotation of 
with centre (0, 0).
It is important, as well, that you know how to write the mapping rule for an initial vector and its image. For example, the coordinates of the head of the unit vector, i, after a rotation of 90°, become (0, 1). This can be illustrated by the mapping rule shown below.
Access to a unit circle that includes all the exact sines and cosines will prove useful for this Investigation, particularly if you are having difficulty recalling all values from memory. Proceed with Investigation 6. Hints and suggestions are provided for use if and when you are experiencing difficulty.
A summary of the Investigation is provided for verification of your general rotation matrix. It is imperative that you have correctly developed this matrix. Otherwise, you will not be successful with the Investigation Questions.
It is important to note that if the angle of rotation is a "special angle," a calculator is not to be used to find the related sine and cosine values. You are expected to know the exact trigonometric values for angles of 30°, 45° and 60°. If, for example, the angle of rotation is 72°, use of a calculator is permitted.
Proceed with the Investigation Questions.
Notebook Entry:Record the general rotational matrix.
For the next lesson, you will need a copy of Blackline master 4.4.1, found on pages 441 to 444 of the Teacher's Resource Book. It might be wise to get this in advance from your on-site teacher. Photocopy each of the four pages and cut out the cards. Have them ready when you begin the next lesson.
Return the Blackline Master sheets to your on-site teacher.
An example is provided below.
Activity
C.Y.U. pages 243 & 244 #'s 11 - 17
When you have completed these questions, ask your on-site teacher to get the solutions for you from the Teacher's Resource Binder and check them against your answers. After you do this, if there is something you had trouble with and still do not understand, contact your on-line teacher for help.
Test Yourself
- Using unit vectors on the unit circle, find the matrix that performs each rotation about the centre (0, 0).
(a) 180°
(b) 60°
(c) 330°
(d)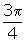
- The vertices of
ABC are A(3, 2), B(-1, 1) and C(-1, 2). A rotation of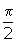 
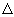about the centre is applied to ABC. Write the general rotational matrix for this rotation, and find the coordinates of the vertices of the image of ABC.
Solutions
2. The general rotation matrix is given by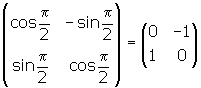 
.
The image vertices are found by multiplying the general rotational matrix by the matrix representing the given triangle, as shown below.
Thus, the image triangle has coordinates A /(-2, 3), B /(-1, -1) and C / (-2, -1).