Learning Resources
Lesson
Focus B: Other Trigonometric Functions
This Focus is short in nature and designed as a refresher, as it reintroduces the reciprocal of sine.
Before beginning the Focus, record the three reciprocal identities for sine, cosine and tangent previously studied in Mathematical modeling, Book 2. You may check your response.
A calculator lesson, should you require one, is provided on evaluating reciprocal trigonometric functions.
Complete Focus B as outlined on page 232 of your text.
Investigation 5: Other Trigonometric Functions
This Investigation allows you to explore some interesting properties of the graphs of the reciprocal trigonometric functions.
Complete the Investigation as outlined on pages 233 & 234 of your text. You would be wise to look for patterns as you draw the graphs.
A summary of the Investigation is provided. You may view it after you have completed all of the Investigation Questions.
Below, you will find a review of the key ideas from Investigation 5 as well as some worked examples that will help you with the Check Your Understanding questions.
Activity
C.Y.U. pages 234 - 236 #'s 16 - 22
When you have completed these questions, ask your on-site teacher to get the solutions for you from the Teacher's Resource Binder and check them against your answers. After you do this, if there is something you had trouble with and still do not understand, contact your on-line teacher for help.
Test Yourself
- Using your knowledge of transformations, describe and sketch the graph of the function y - 5 = sec 2(x -
 ).
). - Why does the graph of secx have local maxima and minima?
- Is y = secx an odd or even function? Why?
Solutions
1. Your explanation should include the following points.
- The period is
 since the horizontal stretch is
since the horizontal stretch is 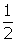 .
. - There is a horizontal translation of
 .
. - There is a vertical translation 5 units up.
- There is no vertical stretch.
- The local maxima occur at
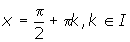 .
. - The local minima occur at
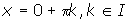
- The vertical asymptotes occur at
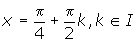
- The graph is shown below.
2. The secant function is the reciprocal of the cosine function. It decreases where cosine increases, and vice-versa. Thus, since cosine has a local maximum and minimum, so must secant.
3. The secant function is an even function since f(x) = f(-x).