Learning Resources
Lesson
Your on-line teacher may allow you to work in pairs or small groups for this Investigation. If so, be sure each of you create your own graphs so you can record your own observations directly on the graph.
Complete Step Aof Investigation 2 on page 218 of your text. Do not proceed any further in the Investigation until you are told to do so.
You will notice that the graphs of the sine and cosine functions are provided in Step A. It is wise to draw the graphs yourself on two different grids. This will allow you to move the graphs as you complete the questions.
Once Step A is completed, graph the equivalent relations. For example, graph
y = cosx and y = cos (-x) on the same graph. A hint is provided to assist you in using the graphing calculator.
You may now proceed to complete the remainder of the Investigation and its questions.
Once the Investigation is complete, plot the original function along with its transformation to verify your findings. You can use your graphing calculator to plot each one in the same graphing window.
Notebook Entry:After Investigation Questions 20 and 21 are completed, record your understanding of odd and even functions. Do this before beginning question #22. Your response should include examples as well as a description of how odd and even functions are alike and different.
Note
You will need the following materials for the next Investigation. Gather them together so you will have them on hand when you are ready to move to the next lesson.
- compass
- protractor
- ruler
- graph paper
- cardboard
- a few straws
- pushpins or thumbtacks
Activity
C.Y.U. pages 219 & 220 #'s 25 - 29
When you have completed these questions, ask your on-site teacher to get the solutions for you from the Teacher's Resource Binder and check them against your answers. After you do this, if there is something you had trouble with and still do not understand, contact your on-line teacher for help.
Test Yourself
- If cosx = 1, find cos(-x).
- If sinx = -
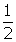, find sin(-x). - Name another function that has the same graph as that of y = sin(-x).
- Name another function that has the same graph as that of y = sin(
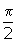+ x). - Find the smallest possible positive angle that could describe a point on the unit circle at (a)
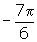(b)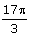 
Solutions
1. cos(-x) = 1 since the cosine function is even.
2. sin(-x) = since the sine function is odd.
3. Answers may vary. Example: y = -sinx
4. Answers may vary. Example: y = cosx
5. (a) 
(b) 