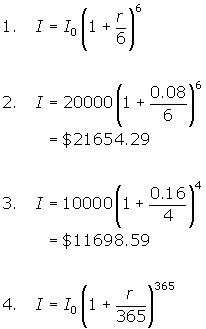Learning Resources
Lesson
Before beginning, a review of exponents and logarithms is necessary. Two problems are given below. Using your previous knowledge from Mathematical Modeling, Book 3, set up and solve each word problem. The correct solution to each example is provided for your viewing after each question is completed.
Example 1
The population at any time, t min, in a bacteria culture is modeled by the function 
. Solve for t.
Example 2
The mummified body of a woman was discovered in a burial mound in Siberia in 1993. It was found to contain 75% of the original carbon-14. What was the estimated age of the mummy, given that the half-life of carbon-14 is 5700 years?
Although the content of this Focus centres around the mathematics of finance, not a lot of detail is provided. The intent is for you to explore various compounding periods and their effect on returns over the year. This will provide the basis for the concept of continuous interest to be introduced in Investigation 8.
Compound interest is interest that is calculated at the end of a given compound period and added to the principal. In the next compounding period, the interest is then calculated using this new amount.
The value of an investment, when the compounding period is one year, is determined by the formula
where:
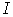denotes the value of the investment at the end of the year 
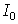denotes the amount of the investment before the interest is added - r denotes the interest rate (as a decimal)
Quite often, however, the interest is calculated more than once a year; perhaps two, four, or even six times. In such situations, an adjustment must be made to the above formula.
If, for example, the interest is calculated twice a year, there are two compounding periods; one every six months. One-half of the annual interest rate is applied to the investment at the end of six months. If the rate is 8%, for example, then a 4% rate is applied after six months. This occurs twice in the year.
Similarly, if interest is calculated four times a year, four compounding periods exist. One-quarter of the annual interest rate is applied at the end of three months. The given interest rate is divided by four before it is applied.
Do you think it would be more beneficial to have interest on an investment compounded annually, semiannually or six times a year? You will be able to verify your response by the end of the Focus.
Read the introduction to Focus L and Example 1 on pages 181to 182 of your text. After reading the given example, you may view a summary of the process involved in calculating the value of an investment, after one year, with n compounding periods.
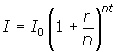
Another example is provided below.
Answer the Focus Questions.
Activity
Focus Questions page 182 #'s 1 & 2
When you have completed these questions, ask your on-site teacher to get the solutions for you from the Teacher's Resource Binder and check them against your answers. After you do this, if there is something you had trouble with and still do not understand, contact your on-line teacher for help.
Test Yourself
- Suppose there are six compounding periods per year for an initial investment, 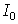, earning an annual rate of r. Write an expression that will give the value, 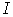, at the end of one year.
- Refer to question #1. What would be the value of a $20 000 investment at the end of the year if the annual interest rate was 8%?
- Find the value of a $10 000 investment, after one year, that pays 16% annual interest compounded quarterly.
- Suppose the interest on an initial investment, 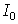, is calculated daily. Write an expression that will give the value of the investment, earning an annual rate of r, at the end of the year.
Solutions
