Learning Resources

Home »  » Courses » Mathematics » Advanced Mathematics 3207 (delisted) » Unit 03 » Set 06 ILO 01 » Go to Work

Lesson

The section opener, on page 177 of your text, shows a graph that relates a salesperson's earnings to the amount of sales. The amount, you will readily determine, is not a single rate. It varies depending upon the amount of sales, as the individual is paid a commission as opposed to a flat rate. This concept should not be a novel one for you and, in fact, some of you may have parents or relatives who are paid based on this principle.

Read the section opener and answer the related questions.

A hint is provided for question #2 for those who may be experiencing difficulty.

Do you recall the piecewise function discussed at the beginning of section 3.5? If not, refer back to page 168 of your text to refresh your memory.

Investigation 7 deals with piecewise functions in more detail. Carry out the procedure as outlined on page 178 of your text. Some hints and suggestions are offered, and should be used only if you have tried each step.

• Step A
• Step B 

Before moving to the Investigation Questions, answer the following questions in your notebook. 

1. Why is there a hole in the graph given in Step A?
2. Is the graph in Step A continuous or discontinuous?
3. How would the equation of the piecewise function change if the open and closed circles on the graph in Step A were interchanged?
4. Will a hole exist in the graph for Step B? Why or why not?
5. Is the graph in Step B continuous or discontinuous?

Verify your answers.

Two examples are provided below that may help with the Check Your Understanding questions.

Activity

C.Y.U. pages 179 & 180 #'s 7 - 15

When you have completed these questions, ask your on-site teacher to get the solutions for you from the Teacher's Resource Binder and check them against your answers. After you do this, if there is something you had trouble with and still do not understand, contact your on-line teacher for help.

Test Yourself

1. Graph the piecewise function .
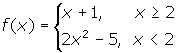2. Refer to your graph from question #1.
   (a) Find .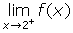
   (b) Find .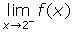
   (c) Find f(2).
   (d) Based on your answers, what can you say about the function at
        x = 2?

Solutions

1. 

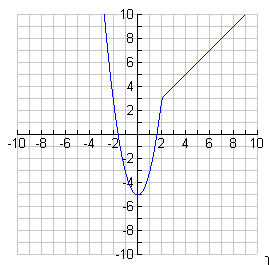
2. (a) 3     (b) 3     (c) 3     (d) The function is continuous at x = 2.