Learning Resources
Lesson
You will investigate the relationship between the graphs of f(x) and |f(x)|. By the end of the activity, you should discover the procedure for graphing |f(x)|, given the graph of f(x).
This Investigation involves the sketching of various graphs. Ideally you should visualize the graphs before you plot them, since they are all of types you have studied in detail. If you use technology to plot the graphs, be sure to sketch them on your own paper as well. In addition, describe the graphs as transformations of similar types.
Carry out the procedure as outlined on page 169 of your text. A suggestion for steps B and D is provided, along with instructions on using the absolute value feature on the TI-83.
Before attempting the Investigation Questions, try the example below.
Graph y = (x + 2)(x -3) on your calculator. Using this graph as a guide, sketch the corresponding absolute-value function.
Once your sketch is complete, verify your results on your calculator.
Once you have completed the Investigation and accompanying questions, you may view a summary if you are confused as to the conclusion that should be made.
Notebook Entry:Record the process for graphing absolute-value functions.
Some examples are provided below.
Activity
C.Y.U. pages 170 & 171 #'s 9 - 11
When you have completed these questions, ask your on-site teacher to get the solutions for you from the Teacher's Resource Binder and check them against your answers. After you do this, if there is something you had trouble with and still do not understand, contact your on-line teacher for help.
Test Yourself
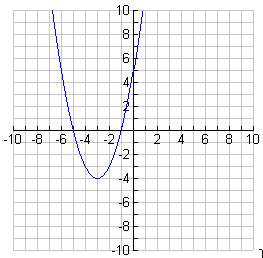
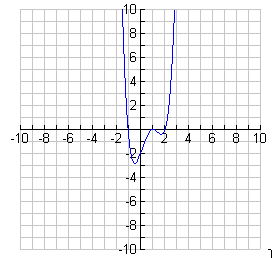
Each graph below shows the graph of some function, f(x). Construct the graph of ![]() .
.
1. 
2. 
3. 
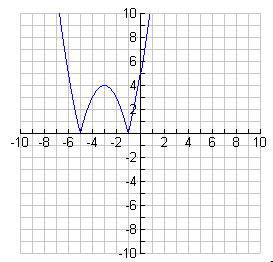
Solutions
1. 
2. 
3.