Learning Resources
Lesson
This Focus centres around the solving of irrational equations. Take for example, the equation 
. Many of you can determine, by inspection, that there is no solution to this problem. Taking the principal square root of a number will result in a positive value, not a negative one. This is indeed the correct solution.
Look again at the above example. You are already certain that there is no suitable solution. Solve the equation algebraically to verify this thought. It is important that you do this task and record the result in your notebook. While this exercise may seem trivial, it is going to prove useful in setting up the concept to be introduced in this section. You may check your solution once you are finished.
Solving the problem algebraically seems to have resulted in a solution of x = 9. This is against our better judgment since, logically, no solution is possible. Let's look further into the situation to see what has transpired.
First of all, let's check the solution of x = 9, to see verify whether or not it works.
Check: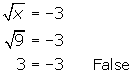 
Clearly, the solution x = 9 results in a false statement. This solution is known as an extraneous root and must be rejected.
- Can you determine why, if there is no solution to the problem, solving it algebraically results in an answer?
- What caused this to happen?
Look back at your solution to help you answer these questions. Examine each step carefully.
You may check your response.
Extraneous roots are often--but not always--introduced when you square both sides of an equation. For this reason, it is imperative that you check all solutions when solving irrational equations. Extraneous roots must be identified and rejected.
Solve the irrational equation below. Don't forget to check all solutions for extraneous roots.
Solve 
. A detailed solution is available to allow you to verify your result.
A summary of the steps used to solve irrational equations is provided.
Read through Focus I on pages 163 to 165 of your text. Answer the related Focus Questions.
Some additional examples are provided below.
Activity
Focus Questions page 165 #'s 28 - 30
C.Y.U. pages 165 - 167 #'s 31 - 39
When you have completed these questions, ask your on-site teacher to get the solutions for you from the Teacher's Resource Binder and check them against your answers. After you do this, if there is something you had trouble with and still do not understand, contact your on-line teacher for help.
Test Yourself
- Can you tell, from inspection, whether or not the equation
will have any extraneous roots? Explain. - Solve
. Check for extraneous roots. - Solve
.
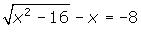Solutions
- Isolating the radical will result in the equation
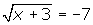. Clearly there is no possible solution, since taking the principal square root of a number will result in a positive answer, not a negative one. Solving the equation algebraically will indeed result in a solution, but it will be an extraneous as it will not satisfy the original equation.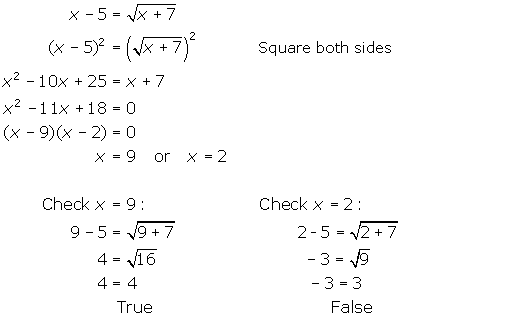 
extraneous root: reject
The only solution is x = 9.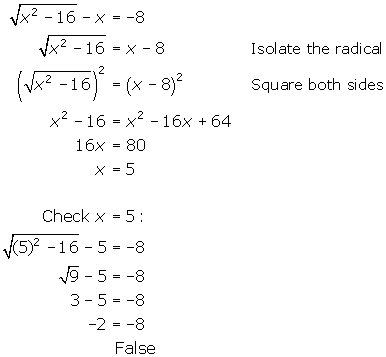
Since x = 5 is an extraneous root, there is no solution to the problem.