Learning Resources
Lesson
During this Investigation you will examine square-root functions and explore how inequalities can be used to determine over which intervals they are continuous.
Begin with the procedure outlined on page 162 of your text. Use of the graphing calculator will speed up the process greatly. Hints and suggestions are provided for various steps should you require assistance.
After completing the Investigation, proceed with the Investigation Question.
A few examples are provided below.
Activity
C.Y.U. pages 162 & 163 #'s 19 - 27
When you have completed these questions, ask your on-site teacher to get the solutions for you from the Teacher's Resource Binder and check them against your answers. After you do this, if there is something you had trouble with and still do not understand, contact your on-line teacher for help.
Test Yourself
- What is the relationship between the functions f(x) = x + 1 and
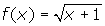? - What inequality must be solved to determine the intervals over which the function
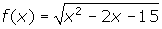is continuous? Discontinuous? - What is the domain of the function
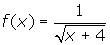? - Determine the interval over which the function
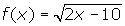is discontinuous.
Solutions
1.
- The square-root function is positive when the original function is positive. (IE: when x
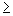-1). - The square-root function is undefined (discontinuous) when the original function is negative. (IE: when x < -1).
- X = -1 is the zero of both the original function and the square-root function.
- The graph of the square-root function will not extend upward as quickly as that of the original function.
2.
- Continuous: (x - 5)(x + 3) 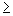0
- Discontinuous: (x - 5)(x + 3) < 0
3. {x / x > -4, x ? R}
4. You must solve the inequality 2x - 10 < 0. The solution is x < 5. Using interval
notation, you can write (-
, 5).