Learning Resources
Lesson
To date, you have acquired many analytical skills with respect to rational functions. A good working knowledge of these skills will allow you to progress through this Focus with little difficulty. A rational inequality, you will realize, can be solved by examining the function produced when the inequality is expressed as one rational expression.
Before beginning the Focus, however, it might be wise to summarize what you have learned thus far about rational functions. Obtain Blackline Master 3.3.1 from your on-site teacher. It is actually page 344 of the Teacher's Resource Book. Completing the table will prove to be an invaluable exercise and study tool. This task must be completed before attempting the Focus.
Suppose you were to solve the rational inequality
.
One approach could be to graph the related rational function 
.
Examination of the graph would identify the intervals over which the function takes on positive values (the values of x for which the inequality is greater than zero).
There is however a faster process by which the solution can be obtained. Since you are not instructed to graph the related rational function, there is no need to do so. Focus again on the above example. Creating a sign graph for the function will allow you to readily identify the intervals over which the function is positive. Although an explanation is offered below, some of you may need to refer back to your work with sign graphs in Chapter 2.
Remember that a sign graph is, in essence, a replica of the x-axis. Follow the steps below to create the appropriate sign graph.
- Find the x-intercepts and vertical asymptotes and mark them on the sign graph. In this case, the x-intercept is 2.5 and vertical asymptotes exist at
x = 7 and x = -4. - Indicate the vertical asymptotes by drawing broken vertical lines through 7 and -4. Indicate the zero by putting a closed circle or X on 2.5.
- The sign graph should now be separated into four intervals. Since each of these values occur an odd number of times (2.5 is a triple root, and 7 and -4 occur once), a sign change will occur as you pass each value on the sign graph.
- While you can choose any test value, zero is a convenient one to select. When x = 0, y is positive. Thus the function has positive values over the interval (-4, 2.5).
- Indicate this on your sign graph and change the sign as you pass -4, 2.5 and 7.
- Since you are interested in values of x that make the function greater than zero, the solution is x ? (-4, 2.5) U (7,
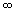). The correct answer is obtained without the use of a graph.
Using the same procedure, you will now attempt to solve 
. No doubt, you have noticed that this inequality is not in the same form as the one in the previous example. To enable usage of the previous process, you must first rearrange the expression bringing all terms to one side. A common denominator is needed to allow you to combine the two expressions into one. The goal is to have only one rational expression on one side of the inequality sign, and zero on the other. Follow the steps below to solve the given inequality.
- Rewrite the expression, bringing all terms to one side, over one denominator.
- Locate the zeros of the function and identify them on a sign graph with a closed circle or X.
- Identify the vertical asymptotes and indicate them on the sign graph using broken vertical lines.
- Select a test value for x. Any one will suffice as long at it is not one of the zeros of the function. Determine if your chosen value results in a positive or negative y-value. Indicate this on the sign graph.
- Complete the remainder of the sign graph accordingly. Remember, if a value occurs an odd number of times, there is a sign change as you pass that value on the sign graph. If a value occurs an even number of times, no sign change occurs.
- Write the solution using interval notation.
Once the task is completed, you may check your solution.
Some of you may be thinking that cross-multiplication would be an easier process by which to solve the above inequality. This is an incorrect method to use when solving rational inequalities. Quite often, this process produces only one of the intervals required. Please make a note of this, as it is a common mistake made by many students.
Read Focus G on pages155 & 156 of your text, paying close attention to the examples given. In example 10, the inequality sign is changed in the last step. Why? Check here if you are unsure of the reason.
Notebook Entry: Record the process used to solve rational inequalities.
Another example is provided below.
Activity
Focus Questions page 156 #'s 36 - 38
C.Y.U. page 156 #'s 39 - 41
When you have completed these questions, ask your on-site teacher to get the solutions for you from the Teacher's Resource Binder and check them against your answers. After you do this, if there is something you had trouble with and still do not understand, contact your on-line teacher for help.
Test Yourself
-
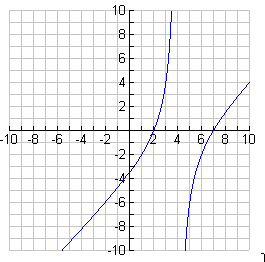
The function
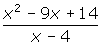is graphed below. Use the graph to solve 
. 
-
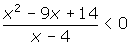Express the inequality
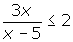as one rational expression. -
Sue is asked to solve
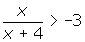. She instinctively uses cross-multiplication and arrives at a solution of x > -3. Is this the correct solution? Explain.
Solutions
1. You are looking to see where the graph is negative. Find the intervals where
the graph is below the x-axis. The correct solution is x ? (-, 2) U (4,7).
2. 
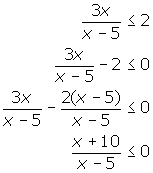
3. It is a common error is to attempt to solve inequalities by cross-multiplication.
This method is incorrect in that it gives only one of the two intervals. The
correct answer is x ? (-, -4) U (-3, ).