Learning Resources
Lesson
In sections 3.1 and 3.2. you graphed rational functions. This Focus makes use of the skills you have acquired, allowing you to visualize and sketch the graphs of rational functions.
Think back to your work with rational functions. How can you, for example, determine the location of points such as the x-intercepts and the vertical asymptotes? How can you find any existing horizontal and oblique asymptotes?
Some of you may need practice on these concepts. Three examples are given below as a means of review of previous material. Remember, it is generally useful to factor rational functions wherever possible.
- Example 1:Determine the vertical asymptotes and/or points of discontinuity for the function
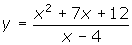. - Example 2: Determine the vertical asymptotes and/or points of discontinuity for the function
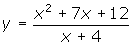. - Example 3: Find the oblique asymptote for the function
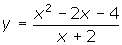
After you complete each problem, you may view the correct solution.
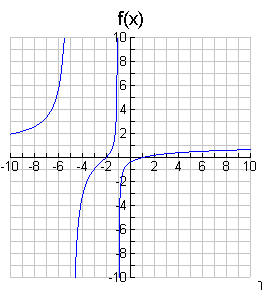
s Focus is split into two parts. It it designed to demonstrate how the vertical and horizontal asymptotes guide the overall shape of the graphs of rational functions. You will use your knowledge of asymptotes, points of discontinuity and zeros to assist you in sketching rational functions.
Read Example 7 on page 151 of your text and answer the related Focus Questions. Then read Example 8 and answer the Focus Questions that follow.
Notebook Entry: Make a note of how to tell whether, and where, a graph crosses of touches the horizontal asymptote.
Activity
Focus Questions pages 151 - 153 #'s 25 - 29
C.Y.U. pages 153 & 154 #'s 30 - 35
When you have completed these questions, ask your on-site teacher to get the solutions for you from the Teacher's Resource Binder and check them against your answers. After you do this, if there is something you had trouble with and still do not understand, contact your on-line teacher for help.
Test Yourself
Consider the function 
.
- Find the zeros and the y-intercept.
- Find the equation of the vertical asymptotes. Will the graph ever cross these asymptotes? Explain.
- Are there any points of discontinuity? Explain.
- Find the equation of the horizontal asymptote.
- Does the graph cross the horizontal asymptote? If so, where?
- Choose and evaluate appropriate test values. A sign graph will be useful. Use the signs of the corresponding function values to help you sketch the graph.
Solutions
- First of all, before answering any questions, you should factor the rational expression to get
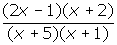. Note: there are no common factors. The zeros of f(x) are the zeros of the numerator, which are x = 
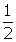and
x = -2. The y-intercept, found by replacing x with 0, is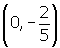
. - The vertical asymptotes, found by examining the zeros of the denominator, are x = -5 and x = -1. The graph never crosses the vertical asymptotes because the function is undefined for these particular values of x.
- There are no points of discontinuity since the zeros of the denominator are not also zeros of the numerator.
- The horizontal asymptote is found by evaluating the limit of f(x) as x approaches
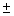
. You can arrive at the answer by inspection. The numerator and denominator have the same degree and the ratio of the leading coefficients is 2. Thus, there is a horizontal asymptote at y = 2. - Since the horizontal asymptote is y = 2, the graph will touch or cross it when y = 2. You must therefore solve the equation
.
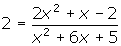Cross-multiplication will lead to the correct answer of x =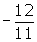
. This is the value of x at which the graph crosses the horizontal asymptote. 