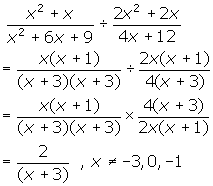Learning Resources

Home »  » Courses » Mathematics » Advanced Mathematics 3207 (delisted) » Unit 03 » Set 03 ILO 01 » Go to Work

Lesson

You have had some previous experience with rational expressions. Focus D is intended as a review of this concept. If you feel comfortable with rational expressions, you may proceed independently through the Focus.

This Focus is presented in two parts. There is a section of questions to answer after examples 1and 2, and more questions to answer after examples 3 and 4. The ideas presented in examples 3 and 4 may be new to some of you, but overall you should have little trouble with the Focus Questions.

To be successful with this Focus, it is imperative that you are able to skillfully perform ordinary arithmetic operations with rational expressions.

Just as you would find a common denominator to add or subtract two fractions, you must also find one to add or subtract two rational expressions. The only difference is that the LCD. will often involve polynomials as opposed to just an integer. Hence, to ensure you correctly identify the LCD., you should first factor each denominator if possible. Doing so will simplify the expression obtained for the LCD.

When multiplying rational expressions, it is essential that you first identify any polynomials that can be factored. Factoring where possible will allow you to make the problem easier by canceling common factors. Failure to factor these expressions will result in a much longer, tedious process often leading to the incorrect result.

To divide two rational expressions, you multiply by the reciprocal. This process is no different than the one for dividing two fractions. Remember to factor any factorable expression before attempting to multiply. This will allow you to identify and cancel common factors.

As well, it is common practice to state any restrictions that exist when simplifying rational expressions. As you are well aware, division by zero is unacceptable in mathematics. Hence, any value of the variable that produces zero in the denominator must be restricted from the domain of the function. You must examine each step of the process carefully when determining such values.

As practice, before beginning the Focus, you might want to answer the questions below. This will be particularly beneficial to those of you who feel your skills on simplifying rational expressions are weak.

  1. Simplify
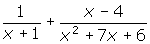
  2. Simplify

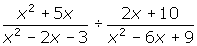
Remember:

  • Before finding a common denominator, factor the denominators if possible.
  • Factor wherever possible before multiplying rational expressions.
  • When dividing rational expressions, multiply by the reciprocal.
  • Record any restrictions on the given variable.

Once the task is completed, you may view detailed solutions.

Study examples 1 and 2 on page 144 and answer the related Focus Questions. Be sure to read the "Note" written in the margin.

Before moving on to examples 3 and 4, you may read the explanations that follow if you require further explanation and practice. These examples involve complex fractions; fractions within fractions.

Think for a moment about the complex fraction .

  • What would be the first step in the simplification process?
  • Since the division of fractions is involved, can you multiply by the reciprocal right away?
  • What is the LCD. for the pair of fractions in the numerator?
  • What is the LCD. for the pair of fractions in the denominator?
  • What is the simplified version of the top pair of fractions?
  • To what fraction does the pair of fractions in the denominator simplify?
  • Simplify the given complex fraction.

You may check your result.

Using the same skills, simplify .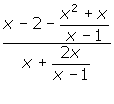

A detailed solution is provided.

Study examples 3 and 4 and answer the Focus Questions.

Two additional examples are provided below.

Activity

Focus Questions pages 145 & 146 #'s 1 - 8

C.Y.U. pages 146 & 147 #'s 9 - 15

When you have completed these questions, ask your on-site teacher to get the solutions for you from the Teacher's Resource Binder and check them against your answers. After you do this, if there is something you had trouble with and still do not understand, contact your on-line teacher for help.

Test Yourself

  1. What is the L.C.D. for the pair of fractions ?
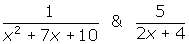  2. What restrictions exist for the rational expression ?
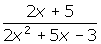  3. Simplify .
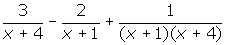  4. Simplify .

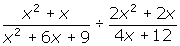Solutions

1. x2 +7x + 10 factors to give (x + 5)(x + 2) and 2x + 4 factors to give 2(x +2). Thus the L.C.D. is 2(x + 5)(x + 2).

2. Since the factors of the denominator are (2x - 1)(x + 3), the restrictions are x , -3.

3.

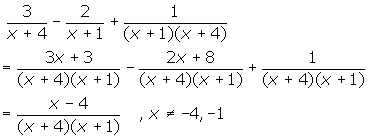
4.