Learning Resources
Lesson
Thus far, you have examined vertical and horizontal asymptotes of rational functions. This Focus, however, introduces the concept of oblique asymptotes. An oblique line, as you may know, is a line with slope other than zero or undefined; neither vertical nor horizontal.
You will examine the graphs of rational functions, with no common factors, in which the degree of the numerator is one more than that of the denominator. You have already discovered that this particular rational expression has no horizontal asymptote due to the fact that its limit as x approaches 
is not a finite number. There will, of course, be vertical asymptotes at the values which make the denominator zero. These particular rational functions however will, in addition to the vertical asymptotes, have an oblique asymptote.
Reflect, for a moment, upon the equations of the asymptotes you have previously studied. Horizontal asymptotes, since they have slope zero, take on the form "y = a constant." Vertical asymptotes are represented by equations of the form "x = a constant" since they have an undefined slope. Oblique asymptotes then, since they are lines with slope neither zero nor undefined, must take on the form y = mx + b.
In actual fact, the equation of an oblique asymptote is given by the quotient of the numerator and denominator (ignoring the remainder). This asymptotic behaviour is explained by expressing the given rational function as the sum of a quotient and a remainder divided by its original denominator. Using your previous knowledge you can conclude that, as the absolute value of x becomes very large, the expression involving the remainder divided by the original denominator becomes very small; approaching zero. Based on this, you can speculate that the oblique asymptote is given by the equation "y = quotient."
Sound confusing? An example will make things clear.
Consider the rational function 
.
Use your knowledge of synthetic substitution and/or long division to find the quotient and remainder. You may check your result to ensure it is correct before proceeding with the remainder of the question.
Based on this result, the given function can now be rewritten as 
.
That is, the given rational function is now written as the sum of a quotient,
(x + 2), and the remainder, 2, divided by the original denominator, (x + 5).
To determine what happens to this function as x approaches , let's explore the behaviour of this function in comparison to that of the quotient, y = x + 2.
Enter the following functions into the Y= menu of your calculator.
- Y1 = x + 2
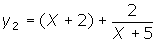
View the TABLE feature to see the accompanying tables of values. A sample screen shot is available for you to view to ensure you are on the right track.
You will notice that the y-values for each function are pretty close. To ensure this is the case, choose larger values for x and examine the resulting y- values. You can, for example, use the TABLE SET feature and set the TblStart to begin at 100. This will allow you to examine the behaviour of each function for larger values of x. Again, a sample screen shot is available for you to view.
Again, you will notice that the results for each function are extremely close. In fact, the larger the value of x, the more negligible the difference between the two y-values. This would imply then that these two function approach the same value as x approaches . This happens because the expression 
approaches zero. You probably already realized this since the degree of the numerator is less than that of the denominator.
As a result, as x approaches , the value of approaches y = x + 2. You can therefore conclude that y = x + 2 is an oblique asymptote for the function. Notice that the oblique asymptote takes the form
y = quotient.
To ensure you understand the process for identifying oblique asymptotes, complete the following question in your note book.
If 
, then why is it that Q(x) is the oblique asymptote for 
?
You may check your solution once you have written your response.
Earlier it was mentioned that since oblique asymptotes are linear, their equation takes on the form y = mx + b. What does this imply about the degree of the quotient?
Any existing oblique asymptote is given by the quotient. Thus, it follows that if the quotient is not linear, there will be no oblique asymptote. The quotient will be linear only if the degree of the denominator is one less than the degree of the numerator.
You should have discovered by now that a solid understanding of vertical, horizontal, and oblique asymptotes can help you sketch rational functions. Correctly finding and plotting them will assist you in graphing the function. The asymptotes are guides for the overall shape of the graph.
Notebook Entry:Record the definition of an oblique asymptote and the process by which they are found.
An example is provided below.
You are now ready to begin Focus C and answer the Focus Questions on pages 141 & 142 of your text.
Activity
Focus Questions pages141& 142 #'s 18 - 23
C.Y.U. pages 142 & 143 #'s 24 - 27
When you have completed these questions, ask your on-site teacher to get the solutions for you from the Teacher's Resource Binder and check them against your answers. After you do this, if there is something you had trouble with and still do not understand, contact your on-line teacher for help.
Test Yourself
- Write the equation of the oblique asymptote for the function given by
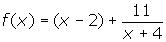. - For
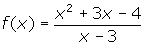, find the quotient and remainder. Use your answer to help you determine the equation of the oblique asymptote. - Will the function
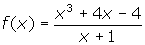have an oblique asymptote? How can you tell?
Solutions
- y = x - 2
- The quotient is x + 6 and the remainder is 14. Since the quotient is linear, the equation of the oblique asymptote is y = x + 6.
- No oblique asymptote exists, since the quotient will be quadratic rather than linear. You should be able to determine this by inspection.