Learning Resources
Lesson
This Focus forces you to consider what happens to various rational functions as x approaches 
, commonly known as the "end" behaviour of the function. The examination of such behaviour provides an indication of where any existing horizontal asymptotes of a function might occur.
First, as a means of review, graph each of the following functions on your graphing calculator:
For each function, use the TRACE feature to help you determine what happens to the y-value as x approaches . Record your results.
You should readily observe that, in each case, y gets closer and closer to zero. In other words, the line y = 0 is a horizontal asymptote. This should be no surprise since the limit, as x approaches , of each of the three functions is indeed zero.
It stands to reason then that if you wanted to determine the horizontal asymptote of a function, you could do so by determining its limits at . The finite number, L, at which you arrive would indicate that a horizontal asymptote exists at y = L.
Most of the rational functions you are to consider in this Focus are such that the degrees of the numerator and denominator are equal. Any such function will have a horizontal asymptote, which can be located by determining the limits at . Many of you are probably thinking of the long, tedious process this would entail; making a table of values for each function to see what happens as x gets arbitrarily large and small.
Although it is not possible to determine the limits by substitution, since you cannot directly substitute , you can avoid the task of creating tables of values. The shortcut you will learn to use hinges on two important concepts.
- As x becomes arbitrarily large, the value of
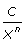(where n is an integer greater than 0) approaches zero. - Dividing every term in both the numerator and denominator by the highest power of x that exists in the denominator generally allows you to eliminate many terms by taking advantage of the previous point.
Suppose, for example, you wanted to find the horizontal asymptote for the function 
.
To do so, you must evaluate 
.
This can be quickly accomplished by dividing every term by 
, the highest power of x existing in the denominator. The process would be as follows:
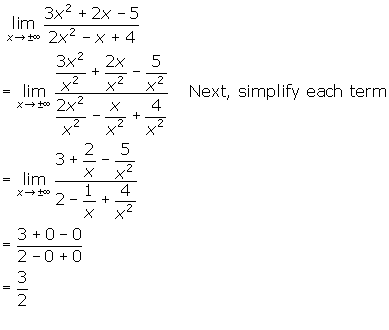
Thus, the horizontal asymptote is y = 
.
In the previous example, the degree of the numerator and denominator were the same.
Consider the function 
in which the degree of the numerator is less than the degree of the denominator.
Find the horizontal asymptote. Do you think this will always be the case? You may verify your result once you have completed the task. Then answer the questions below.
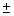
- What do you think would happen if you evaluated the limit as x approached of a function in which the degree of the numerator was higher than that of the denominator?
- Would you get a finite answer for the value of the limit?
- Would a horizontal asymptote exist?
If you are presently uncertain of the answers to these questions, evaluate 
. This task should help you arrive at the answers. You may verify your solution.
You are now more than ready to begin Focus B on page 138 of your text. Read the Focus and proceed with the questions. Refer back to these few Web pages for assistance if you run into difficulty.
Notebook Entry: Record your understanding of how to determine any existing horizontal asymptotes of rational functions.
Once you have completed Focus B, you may want to look at the following examples.
Activity
Focus Question page 139 #'s 8 - 10
C.Y.U. pages140 & 141 #'s 11 - 17
When you have completed these questions, ask your on-site teacher to get the solutions for you from the Teacher's Resource Binder and check them against your answers. After you do this, if there is something you had trouble with and still do not understand, contact your on-line teacher for help.
Test Yourself
- Find the horizontal asymptote of the function
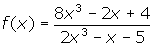. - Determine the horizontal and vertical asymptotes of the function
.
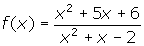Solutions
1. Horizontal asymptote; y = 4
2. Remember: Simplify the function before finding any asymptotes.
- Horizontal Asymptote: y = 1
- Vertical asymptote: x = 1
- Because (x + 2) is a factor of both the numerator and denominator, the function has a point of discontinuity at x = -2.