Learning Resources
Lesson
The previous section involved extensive work with rational functions in which the numerator was a constant. A solid understanding of this concept is an essential foundation on which to enter this section of material. For review purposes, answer the following questions based on the function 
.
- What are the zeros of the function?
- What are the equations of the vertical and horizontal asymptotes?
- What happens to f(x) as x approaches:
(a) infinity
(b) negative infinity
(c) 4 from the right
(d) 4 from the left
(e) -4 from the right
(f) -4 from the left
You may check your answers before moving on to the Investigation.
What do you think might happen if the constant numerator were replaced with a polynomial expression of x? How would this change affect the asymptotes? The zeros? The intervals of increase and decrease? These properties will soon be investigated.
A rational function is any function that can be written in the form y = 
, where f(x) and g(x) are polynomials and g(x) 
0.
Before you can begin to understand and analyze the behaviour of rational functions, you must first have a formalized understanding of continuity. Read the introduction to Investigation 3 on page 136 of your text, examining carefully the graphs in the margin as you go along. Once your reading assignment is completed, you may view a summary of three simple steps that can be used to determine whether or not a function is continuous.
Consider the following piecewise function.
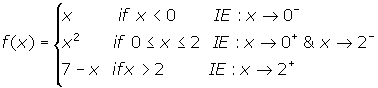
Test f(x) for continuity at x = 0 and x = 2. Once you have completed this task, you may check your solution.
Reflect for a moment on the functions you studied in 3.1. Were they continuous everywhere? If not, where were they discontinuous?
Proceed with the Investigation and questions. As you progress through each step, ask yourself, "What role do the factors of the numerator and denominator play in the graphs of rational functions?" You will notice that each function you graph in this Investigation will be discontinuous at some value of x. Pay particular attention to how the discontinuities you observe in Step A differ from those observed in Step B. You might want to plot each function using technology, and then sketch the curve on your own paper.
The functions given in Step B all result in graphs with "holes" or points of discontinuity. These may often be difficult to see with the graphing calculator. There is, however, a WINDOW setting that is quite useful for displaying the discontinuity. It is shown below. Please make a note of this "friendly window."
Upon close examination of a graph, once this window setting is used, you will see a break in the graph, indicating a point of discontinuity. As well, you can use ZOOM and TRACE to observe the behaviour of the function near the discontinuities.
Once you have completed the Investigation, you may verify your findings for each step.
Before beginning the Check Your Understanding section, you may view a summary of the Investigation if the concept of discontinuity is still unclear.
Notebook Entry: Record the following:
- definition of a rational function
- conditions under which a function, f(x), is continuous
- how to determine points of discontinuity
Two examples, similar to the Check Your Understanding questions, are provided below.
Activity
C.Y.U. pages 137 & 138 #'s 3 - 7
When you have completed these questions, ask your on-site teacher to get the solutions for you from the Teacher's Resource Binder and check them against your answers. After you do this, if there is something you had trouble with and still do not understand, contact your on-line teacher for help.
Test Yourself
- How do the graphs of f(x) = x + 2 and
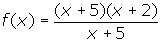differ? - Write
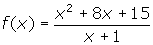in factored form. Determine the vertical asymptotes and any points of discontinuity. - Given
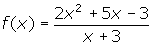. Determine the vertical asymptotes and points of discontinuity. As well, evaluate the one-sided limits at each point of discontinuity. - Write the equations of two functions that have vertical asymptotes at x = 2.
- Write the equations of two functions that have points of discontinuity at x = 2.
Solutions
- The graph of the first function is a line with x-intercept -2, y-intercept 2, and slope 1.The graph of the second function resembles the first, except it has a hole at x = -5 since f(-5) is undefined.
-
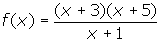. There is a vertical asymptote at x = -1, as a result of the factor of (x + 1) in the denominator only. There are no points of discontinuity. - Remember, before finding any asymptotes, simplify the given expression. This expression simplifies to f(x) = 2x + 1. There are no vertical asymptotes. There is a point of discontinuity at x = -3 since f(-3) is undefined.
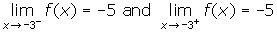. - Answers may vary. Sample functions are given below.
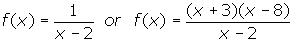
Any answer is acceptable as long as the function contains a factor of (x - 2) in the denominator and, if (x - 2) is also present in the numerator, it occurs to a lesser degree than it does in the denominator. - Answers vary. Sample functions are given below.
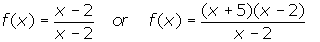
Any answer is acceptable as long as the factor of (x - 2) occurs in the numerator to an equal or greater degree than it does in the denominator.