Learning Resources

Investigation 11: Graphing a Polynomial Function

Investigation 11: Graphing a Polynomial Function

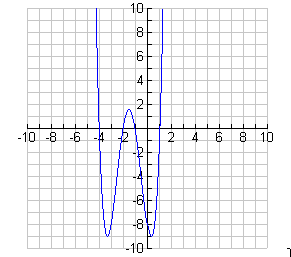
Find the x-intercepts by setting f(x) = 0. Using the Rational Root Theorem and Synthetic Substitution, you will find that x = 1 is a root of f(x). The resulting depressed equation is x³ + 7x² + 14x + 8 = 0. The use of the Rational root Theorem and Synthetic Substitution again, will show that x = -1 is a root. The depressed equation is x² + 6x + 8 = 0, which can be factored as (x + 4)(x + 2). Thus, there are four x-intercepts; 1, -1, -4 and -2. The y-intercept is -8.

A sketch of the curve along with a table of values is provided below. 

f(x) = x⁴ + 6x³ + 7x² - 6x - 8