Learning Resources
Lesson
This Focus is intended to illustrate the different forms in which a derivative can be written. Read the Focus on page 97 of your text and record the different forms in your notebook. As well, answer the Focus Questions.
An explanation of the various notations used to represent the derivative of a function is given below.
- The notation y / is read "y prime."
- The notation f /(x) is read "f prime of x" and it emphasizes the fact that the slope of the tangent line at x is a function of x that is derived from the function f.
- The notation
reads "the derivative of y with respect to x."
The process for finding a derivative is called differentiation. It may be beneficial to think of differentiation as an operation that, when applied to a function f, produces a new function f /.
To understand the general formula for calculating the derivative of f(x) given in the text, it is imperative that you realize that the slope of 
is equivalent to 
, the formula for the slope of a line.
From your work with Investigation 8, you should connect the idea that 
is equivalent to .
The given formula represents the derivative since it represents the slope of a secant as its intersection points with the curve become closer and closer together. As h approaches 0, the slope of the tangent can be found from the limit of the slopes of the secants. The derivative is merely another name for the slope of the tangent to the graph at a point.
Notebook Entry: Record the general formula for the derivative of f(x) in your notebook.
Activity
Focus Questions page 97 #'s 10 & 11
C.Y.U. page 98 #'s 12 - 14
When you have completed these questions, ask your on-site teacher to get the solutions for you from the Teacher's Resource Binder and check them against your answers. After you do this, if there is something you had trouble with and still do not understand, contact your on-line teacher for help.
Test Yourself
- Given f(x) = 3x3 - 9x2 + 7 and f /(x) = 9x2 -18x. Find the equation of the tangent to the graph at the point (1, 11).
- Find the equation of the tangent to the graph y = 3x2 - 2x at x = 4.
Solution
1. The expression f /(x) = 9x2 -18x represents the slope of the tangent. f /(1) = -9 which is the slope of the tangent line at the given point. To find the y-intercept, use the equation y = mx + b, substituting (1, 11) in for x and y. Since m = -9, you will get a value of 20 for b.
Solution: y = -9x + 20.
2. To find the equation of the tangent line, you need to find its slope and
y-intercept.
The slope of the tangent = f /(x)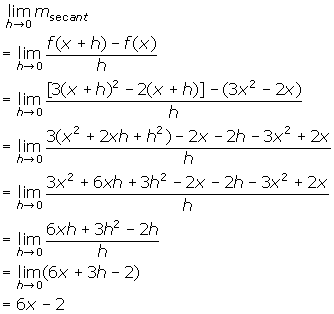 
- This expression represents the slope of the tangent. You must find the equation of this line when x is 4.
- >f /(4)> = 6(4) -2 = 22. This is the slope of the line you are looking for.
- To find the y-intercept of the line, use y = mx + b.
- Since f(4) = 3(4)2 - 2(4) = 40, you know the point (4, 40) is on the line. y = 22x + b. Substitute (4, 40) for x and y. This will give b = -48.
- Thus, the equation of the tangent line is y = 22x - 48.