
Learning Resources
Lesson
Record in your notebook how a tangent line at a point might be defined. Draw an accompanying example as well. After completing this task, you may verify your thinking.
To see how to properly define a tangent, an interactive demonstration using Geometer's Sketch Pad is provided.
The purpose of Investigation 8 is to find the slope of the tangent at any point on a graph of a polynomial function. Working in small groups or pairs is recommended while exploring this activity. Consult with your on-line teacher for direction on the organization of groups.
Before working through the steps of the Investigation, read the introduction on page 95 of your text and answer the "Think about..." question in the margin. Use the language of limits in your explanation. After recording your answer, check for confirmation.
Carry out the procedure and answer the related Investigation Questions. Hints are provided for each step. Use them only if you are experiencing difficulty.
You should now realize that the equation you discovered is indeed the slope of the tangent at any point on the graph of the given polynomial function.
Notebook Entry: Record the definition for the derivative.
Activity
C.Y.U. pages 96 & 97 #'s 7 - 11
When you have completed these questions, ask your on-site teacher to get the solutions for you from the Teacher's Resource Binder and check them against your answers. After you do this, if there is something you had trouble with and still do not understand, contact your on-line teacher for help.
Test Yourself
- Find the equation of the slope of the tangent to the graph y = 2x2 - 1 at a point by definition.
- Find the slope of the tangent to f(x) = 2 - x2 at x = 4.
- The height, above the ground, of an object propelled upward from a rooftop 100 m high with an initial velocity of 80 m/s is given by the function h(t) = 100 + 80t - 5t2. Find the velocity of the object at the end of the first two seconds.
Solutions
1. 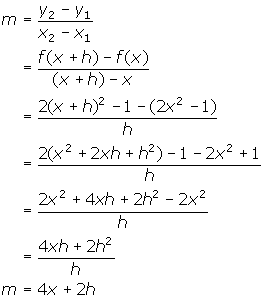
This is the formula for the slope of the secant joining the points.
Slope of the tangent = ![]()
2. 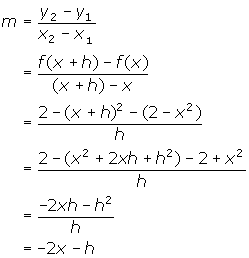
Slope of the tangent = ![]()
At x = 4, the slope of the tangent is -2(4) = -8.
3. You must find the formula for the tangent at a point by definition. Then use
your answer to find the instantaneous velocity at 2 seconds.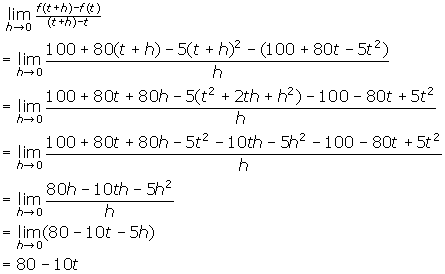
The instantaneous velocity at t = 2 is 80 - 10(2) = 60 m/s.