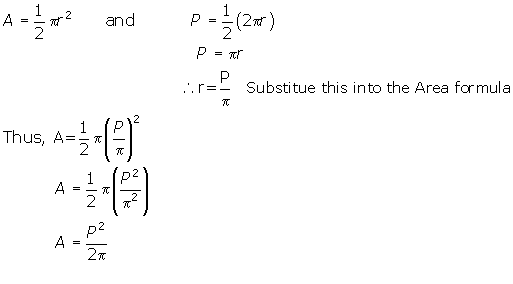Learning Resources
Lesson
Before beginning the Investigation, it is necessary to review some background information on composite functions. Read page 85 of your text. Do not proceed to the Investigation until you are told to do so.
After completing the assigned reading, you may view a summary of the introduction. You will find this beneficial if you had difficulty understanding composite functions.
You have actually been composing functions while transforming graphs using two or more steps. Take, for example, the function 4f(x) - 1. Its graph is obtained by first stretching the graph of f(x) by a factor of four to get a new image. One is then subtracted from the new y-values to slide the graph down one unit.
To ensure your understanding of how composition of functions works, do the questions below in your notebook before moving on to the Investigation. Questions 2 & 3 provide some practice on rearranging formulas, a necessary skill for success with this lesson.
1. Given f(x) = 2x2 - 2 and g(x) = 3x -1. Find f(g(x)) and g(f(x)).
2. Express the radius, r, of a circle as a function of the circumference, C.
3. Use your answer in question #2 to help you express the area, A, of a circle
as a function of the circumference, C.
You are now ready to begin Investigation 6. You will need the following materials.
- 5 different sizes of balls
- a measuring tape or string
- a metre stick
This Investigation is best done in pairs or small groups. If you have other people at your site, group yourselves and follow the procedure as outlined on page 86 of your text.
Hints and suggestions are provided for each step of the Investigation. Use them only if necessary.
A summary of the Investigation is provided. View it after you have completed all steps.
It's time now to discuss some of the symbolism that is associated with the composition of functions. F(g(x)), read "f of g of x," can also be written as f o g as another way of communicating the composition of functions. The notation
f o g means the composition of f with g and is read "f composed with g." The expression (f o g)(x) is equivalent to f(g(x)).
What does it mean to have the composition of functions expressed as
g o f or f o f ?
Before answering the Investigation Questions, do the activity below to help you visualize the composition of functions using graphs. It will also prove useful as you attempt the Investigation Questions. Carefully follow each step below.
- Graph f(x) = 2(x + 4)2 and g(x) = -0.5(x - 5)2 + 4. Be sure to label each graph.
- Choose any value, such as x = 2.
- Evaluate g(2) from the graph of g(x).
- Draw the horizontal line y = g(2) = -0.5 to y = x. Draw the vertical line
x = -0.5 through this intersection point. This changes the y-value -0.5 to an x-value of -0.5. - Evaluate f(-0.5), using the graph of f(x).
You are now ready to complete the Investigation Questions.
Activity
C.Y.U. pages 86 & 88 #'s 1 - 11 and 13 - 17
When you have completed these questions, ask your on-site teacher to get the solutions for you from the Teacher's Resource Binder and check them against your answers. After you do this, if there is something you had trouble with and still do not understand, contact your on-line teacher for help.
Test Yourself
- If f(x) = 2x - 1 and g(x) = 3 - x - x2, find the following:
(a) f(g(1))
(b)g(f(-2))
(c) g(g(o))
(d) f(f(-4)) - Given f(x) =x2and g(x) =
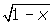. Find f(g(x)) and state its domain and range. - Express the area, A, and perimeter, P, of a semicircular region in terms of the radius, r. Then express A as a function of P.
Solutions
1. (a) f(g(1)) Look at the g(x) function and replace x with 1.
= f(1) Look at the f(x) function and replace x with 1.
= 1
(b) g(f(-2)) Look at the f(x) function and replace x with -2.
= g(-5) Look at the g(x) function and replace x with -5.
= -17
(c) g(g(0)) Look at the g(x) function and replace x with 0.
= g(3) Look at the g(x) function and replace x with 3.
= -9
(d) f(f(-4)) Look at the f(x) function and replace x with -4.
= f(-9) Look at the f(x) function and replace x with -9.
= -19
2. Note: The domain of f(x) is the set of all real numbers.
The domain of g(x) is {x / x 
1}.
The domain of f(g(x), then, is limited to the restriction on the domain of
g(x).
f(g(x)) Replace the expression g(x) with its given expression.
= f( ) Look at the f(x) function and replace x with .
= ()2
= 1 - x
- Domain: {x / x 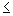1}
- Range: {x / x
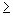0} - Remember: the range of f(g(x)) is now determined by its domain values, which are all real numbers less than or equal to one. If you use only these values for in the expression (1 - x), you will always get answers greater than or equal to zero.
3. 