Learning Resources
Lesson
This Investigation should be relatively straight forward since you have done a lot of work with the use of sign graphs to date. Just as for quadratic inequalities, you will establish a method of solving a cubic inequality using a sign graph. The sign of each interval on either side of the zeros of the corresponding polynomial function must be determined.
Follow the procedure of Investigation 4 as outlined on pages 80 & 81 of your text. As well, complete the Investigation Questions. Some hints are offered. Use them only if you are experiencing difficulty.
If you are having trouble finding the roots of the volume equation, you may view a hint.
After completing Step B, you may view a graph of the polynomial function. It may help you see if you are indeed on the right track. As well, be certain that you understand why it is that you are using a sign graph and locating the roots of the function. Think about how this will assist you in solving the polynomial inequality.
After completing Step D, you may verify your solution.
Complete the Investigation Questions.
Activity
C.Y.U. pages 81 & 82 #'s 47 - 54
When you have completed these questions, ask your on-site teacher to get the solutions for you from the Teacher's Resource Binder and check them against your answers. After you do this, if there is something you had trouble with and still do not understand, contact your on-line teacher for help.
Test Yourself
- Use a number line to solve the inequality (x + 1)(x - 4)(x + 3) > 0.
- For what values of x is the graph of y = 2x3 - 5x above the graph of y = -x2 - 2?
Solutions
1. x ? (-3,-1) U (4, 
)
2. 
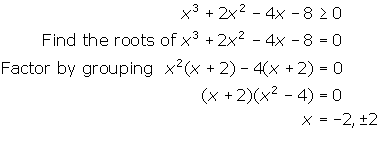
Note that -2 is a double root. Thus, there is no sign change as you pass this
root. As well, bear in mind that you are finding all values of x for which y is
greater than or equal to zero.
Solution: x ? [2,) U x = -2. Note that -2 & 2 are included in the solution.
3. You must solve the inequality 2x3 - 5x > -x2 - 2.
You must find the roots of 2x3 + x2 - 5x + 2 = 0.
The first root can be found using the Rational Root Theorem and the Factor
Theorem. The depressed equation is a factorable quadratic equation.
The roots are 1, -2 ,
. Solution x ? (-2, ) U (1, ).