Learning Resources
Lesson
To date, you have found the roots of a polynomial equation by first graphing the polynomial equation. However, as you probably surmised by now, this is not always the most practical way. Graphing technology may not always be readily available and, as well, there will be times when an equation is sufficiently complex that sketching will not be practical. As a result, we need alternate methods for determining the roots of a corresponding equation and for solving polynomial equations. Once the roots are found, of course, you know the x-intercepts of the corresponding graph and can then determine its shape.
This Focus is designed to provide a technique for solving polynomial equations by factoring. Obviously, the first step in determining the factors of a polynomial algebraically, is to first find a root of the equation. Although this can be done by trial-and-error substitution of integer values for x, it is far more efficient to use the Rational Root Theorem to find possible values for the root and then substitute to check. Synthetic Substitution, an alternate method for finding a root, will also be looked at. Once a root is found, you can use the Factor Theorem to find a factor of the polynomial.
Let's start with the Factor Theorem. You should realize by now that the roots of an equation determine its factors. For example, if x = 4 and x = -2 are the roots of a given quadratic function, its equation can be easily found. Write the equation in you notebook. Verify your result.
So, as you are well aware, once you know the roots of an equation, you can readily determine the factors. The problem is, however, that the roots are not always quickly found. In the previous example, you were given the two roots needed to determine the factors and, hence, the equation.
How would you even begin to find the roots of an equation such as
2x3 - 5x2 - 4x + 3 = 0? Perhaps you might try a few values at random to see if you can locate one that, when substituted in for x, would give the desired result of zero. This is definitely not a recommended process as it's far too time consuming. Besides, what if the roots were fractions that you would never think of trying? There has to be an easier, more efficient way to find the roots of an equation! Welcome to the Rational Root Theorem!
The Rational Root Theorem states that given P(x) is a polynomial of degree n with integral coefficients such that 
, where a is the leading coefficient and a0 is the constant term, a 
0 and a00.
If x = 
is a rational root of P(x) = 0, then:
- m is a factor of the constant term, a0, and
- n is a factor of the leading coefficient, a.
Although this may seem confusing, the theorem is quite easy to apply. Take, for example, the equation used in the above example, P(x) = 2x3 - 5x2 - 4x + 3 = 0. We no longer have to use trial-and-error to find a root. If indeed any rational roots exist, they can be found using the Rational Root Theorem. It might be helpful to first list the possible values for both m and n.
Since m is a factor of the constant term, 3, its possible values are 
1 and 3. Since n is a factor of the leading coefficient 2, its possible values are 1 and 2. Thus the possible rational roots of the equation are all the combinations of
x = , namely x = 
.
Determining which one of these eight values is actually a root of the equation is simply a matter of substitution.
- P(1) = -4, so x = 1 is not a root.
- P(-1) = 0, so x = -1 is a root. Thus, by the Factor Theorem, (x + 1) is a factor. The first factor of the equation has been found. You will see how to find the remaining factors soon. You're probably thinking "Why not just use substitution to find them?" This method is not practical and a more efficient process will be shown.
Before continuing on to explore the process of finding the other roots, you need to review the process of long division, something you, in all likelihood, have not seen since Elementary School.
Suppose little Johnny has to divide 156 by 5, without the use of a calculator. Do this problem in your notebook. As well, see if you can correctly identify the proper names of the pieces of this long division process.
Although this task may seem trivial, it is imperative that you first do the problem before checking the result. Failure to do complete this process may impede your understanding of what is to come next. After completing the task, you may view the correct solution.
Read Step B, Method 1 only, on page 75.
If you require extra practice on long division, a step-by-step look at the process is provided.
If you find this process tedious, there is an alternate, faster method you can use called synthetic substitution. This is a short-cut method of dividing a polynomial by a divisor of the form x - a. It involves working only with the numerical root and the coefficients of the polynomial. The process is similar to long division, but no subtraction takes place.
Read through Method 2, after which you should be ready to answer the Focus Questions. If you feel the need for another step-by-step example, the above long division problem is solved using synthetic substitution.
Often a polynomial is missing a term. In such cases, you must supply a coefficient of zero to the missing term. This holds true for both long division and synthetic substitution.
Divide x3 +2x - 1 by (x + 2). Once you have completed the task, you may verify your solution.
A summary of synthetic substitution is provided.
Answer the Focus Questions on page 76 of your text.
Activity
Focus Questions page 76 #'s 24 - 28
C.Y.U. pages 76 - 78 #'s 29 - 36 & 38, 39
When you have completed these questions, ask your on-site teacher to get the solutions for you from the Teacher's Resource Binder and check them against your answers. After you do this, if there is something you had trouble with and still do not understand, contact your on-line teacher for help.
Test Yourself
- List the possible rational roots of 4x3 -8x + 5 = 0
- If (x+5) is a factor of 3x3 - 2x2 - kx + 1, find the value of k.
- Find the factors of 2x3 + 13x2 +17x - 12.
- Examine the synthetic substitution below and identify the quotient, remainder, divisor and dividend.
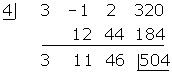
Solutions
-
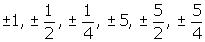
If (x + 5 ) is a factor, then -5 must be a root and the remainder must be 0.
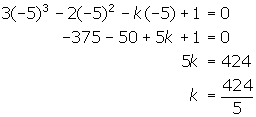
- The possible rational roots are
.
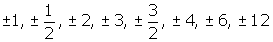-3 is a root since when substituted in for x, it produces a result of zero. Synthetic substitution can be used to find the remaining factors.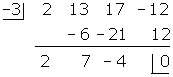
The depressed equation is 2x2 + 7x - 4 = 0, the factors of which are
(2x -1) and (x + 4). Thus, the factors of the given polynomial are (x + 3), (2x - 1) and (x + 4).
- Quotient: 3x2 + 11x + 46
- Remainder: 504
- Divisor: x - 4
- Dividend: 3x3 - x2 + 2x + 320