
Learning Resources
Lesson
Before attempting this investigation, sketch the following polynomial functions on your graphing calculator to again familiarize yourself with the shapes of cubic and quartic functions. Try to visualize the shape of the graph, and in which quadrants it will be located, before you view the actual graph.
- y = (x - 2)(x + 1)2
- y = -(x - 3)2(x + 2)
- y = (x - 1)(x + 4)(x + 1)
- y = (x + 3) (x - 1)2(x - 2)
- y = -(x + 2)3(x -1)
- y = x(x - 4)(x + 2)(x - 1)
This Investigation will establish the method for using the graph of a corresponding polynomial function to solve a polynomial equation. You will then extend this procedure to include the solution of polynomial inequalities.
As you proceed through Investigation 3, drawing the two given graphs in your notebook will prove to be an asset. Begin the Investigation as outlined on pages 70 & 71 of your text and answer the Investigation Questions that follow.
After the extensive work you have done with solving quadratic inequalities, this Investigation should pose little difficulty for you. If, however, you are having trouble visualizing the solution for Step B, a hint is provided.
If you are experiencing difficulty with the Investigation Questions, you should refer back to Focus B before contacting your on-line teacher. Question #3 is particularly important as it provides a summary of the process involved in solving polynomial equations. Be sure to record your answers to all three Investigation Questions in your notebook. Do not proceed any further until you have completed this task.
After the Investigation is completed in its entirety, you may view a summary.
Activity
C.Y.U. pages72 - 73 #'s 14 - 23
When you have completed these questions, ask your on-site teacher to get the solutions for you from the Teacher's Resource Binder and check them against your answers. After you do this, if there is something you had trouble with and still do not understand, contact your on-line teacher for help.
Test Yourself
- Use the graph below to answer the questions that follow.
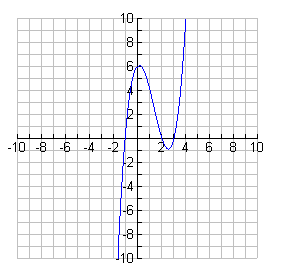
(a) What are the roots?
(b) Use the roots to state a possible equation and adjust the equation to agree with the graph. - (a) Find the x and y-intercepts of y = (x - 2)( x + 3)(x - 1)
(b) Solve the inequality (x - 2)(x + 3)(x - 1) > 0 - Explain how the location of the y-intercept of the polynomial in part (a) of the above question helped to determine the solution to the inequality in part (b).
Solutions
1. (a) The roots are x = -1, 2, 3
(b) The factors are (x + 1), (x - 2), and (x -3) and the y-intercept is 6.
Equation: y = x3 - 4x2 + x + 6
2. (a) x-intercepts: 2, -3 and 1
y-intercept: 6
(b) Solution: x ? (-3, 1) U (2, ![]() )
)
3. The location of the y-intercept can be used to help determine the intervals in
which the graph is above or below the x-axis. Here the y-intercept is positive,
so the graph must be above the x-axis in the interval that includes x = 0.
Since the x-intercepts are 2, -3 and 1, the graph is above the x-axis in the
interval x ? (-3, 1). The graph will, therefore, be below the x-axis in the
intervals on either side of this interval. Hence, we know that the function is
greater than 0 in the intervals x ? (-3, 1) U (2, ![]() ).
).