Learning Resources
Lesson
As discussed in the Overview, this section deals with the combining of functions. Can you think of any reasons functions need to be combined? Make a list of some possibilities.
If you are having trouble getting started, a few examples are provided.
Now that you can see the need for combining functions, you are ready to begin the Investigation.
Investigation 1: Total earnings
This Investigation is self explanatory. Darcy works two jobs, each of which are described for you. His goal is to save at least $50 a week and your task is to determine how many hours he must work to do so. First of all, you will have to create a function to represent his total earnings from the two jobs. Then you will analyze this function to solve the given problem.
Begin the Investigation as outlined on pages 56 & 57 of your text and answer the accompanying questions. A hint to help you determine the domains and ranges is provided. Use it only if you experience difficulty.
When you combine functions, it is important to understand what it is that the combined function represents and how its graph is related to the graphs of the original functions.
Focus A: Combination by Subtracting
In the previous investigation you have seen how two functions can be combined by adding. This Focus requires you to plot the graph of h(x), a new function created by subtracting two functions f(x) and g(x).
You should proceed through this Focus with relative ease, as it is a natural extension of the previous Investigation. Be sure to answer the Focus Questions after you carry out the procedure.
Some hints are offered for Focus Question #5. Use them only after you have attempted the question and only if you had trouble with the tables.
Graphing technology may be used to graph combinations of functions such as required in Focus Question #9. This can be done using the Y= and Y-VARS features. Detailed instructions on this process are provided.
After you have completed the Investigation and Focus, as well as all related activities, you may view a short summary.
Activity
Investigation Questions page 57 #'s 1 - 3
Focus Questions page 58 #'s 4 - 6
C.Y.U. pages 58 - 60 #'s 7 - 14
When you have completed these questions, ask your on-site teacher to get the solutions for you from the Teacher's Resource Binder and check them against your answers. After you do this, if there is something you had trouble with and still do not understand, contact your on-line teacher for help.
Test Yourself
- If f(x) = 2(x + 4) and g(x) = -(x + 5), find x when f(x) + g(x) = 20.
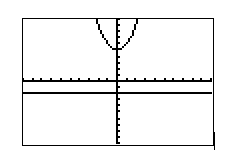
- Examine the graphs below. What do you think the graph of f(x) + g(x) will look like?
- Given f(x) = 2x2and g(x) = 3x - 2. Find the x and y-intercepts of the graph of f(x) + g(x).
Solutions
1. 
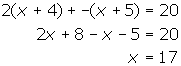
2. The graph of f(x) + g(x) will be a parabola. Its range will depend upon the y-value at the vertex. The graph opens upward and has vertex (0,3).
(IE: f(0) + g(0) = 5 + -2 = 3). Thus, the range is 
. Since there is no restrictions on the domain of either original function, the domain of f(x) + g(x) is {x / x ? R}
3. There are various ways to approach this question. Two methods are shown below.
Method 1: To find the y-intercept, let x be 0 in each function and add the
results. Similarly, to find the x-intercept, let y = 0.
y-intercept: f(0) + g(0) = 0 + -2 = -2
x-intercept: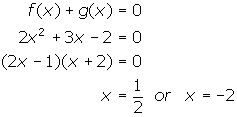 
Method 2: You can combine the two functions first and then find the x and
y-intercepts of the new function, f(x) + g(x).
y-intercept: -2
x-intercept: 