Learning Resources

Home »  » Courses » Mathematics » Advanced Mathematics 3207 (delisted) » Unit 01 » Set 04 ILO 03 » Go to Work

Lesson

In this Investigation, you will learn how to approximate the area of a region under a curve by drawing rectangles between the curve and the x-axis. It is the area of these rectangles that will help you determine the area under the curve. The concept of limit will be used to get an exact value for the area.

You will need graph paper to plot the graphs.

The Investigation is a bit tedious and may be done in pairs. If you choose to work in pairs, each of you must record the findings in your own notebook.

Read the two paragraphs introducing the Investigation on page 36 of your text.

Why is it that the area under the curve indicates a total distance of 20m?

Before beginning the procedure, read the Note in the margin on page 36 of your text.

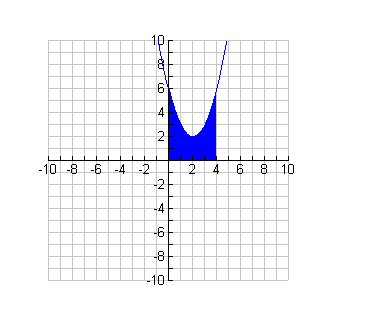
In the graph below, the shaded region represents the area under the curve, from x = 0 to x = 4. Notice that it does not continue below the x-axis.

Carry out the procedure for the Investigation. For convenience, it is best to use a scale of 0.1 on the axes of the graphs you are to draw. Otherwise, the drawings will be too small to do some of the required calculations. Again, a few hints are provided to assist you if you run in to problems during the Investigation. Use them only after you have tried the Procedure but experienced some difficulty.

Complete the Investigation Questions.

If you are still having difficulty with this investigation, or you want to check your work, use the demo below.

Activity

C.Y.U. page 38 -44 #'s 41 - 44

When you have completed these questions, ask your on-site teacher to get the solutions for you from the Teacher's Resource Binder and check them against your answers. After you do this, if there is something you had trouble with and still do not understand, contact your on-line teacher for help.

Test Yourself

Find the area under each curve given below.

  1.  y = 3x2, for   
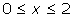
  2.  y = 3(x + 2)2, for  
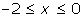
  3.  y = (x - 3)2, for

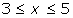
Solutions

1. 

  • The curve y = 3x2 represents a stretch of the curve y = x2.
  • In question #40 you found the area of y = x2, for 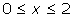to be .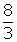 
  • Thus, the answer is  .

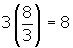2. 

  • This curve is a translation of the curve y = 3x2 by 2 units. 
  • The area between 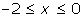for the curve y = 3(x + 2)2 is equivalent to the area between  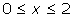 for the curve y = 3x2. 
  • In part (a), you found this area to be 8.

3. 

  • The curve y = (x - 3)2 is a translation of the curve y = x2 by 3 units. 
  • The area between x = 3 and x = 5 is equivalent to the area under the curve y = x2 between x = 0 and x = 2. 
  • Hence, the answer is  .
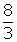