
Learning Resources
Lesson
The notion of limit is basic to a study of calculus. In this Investigation, you will explore a physical situation that suggests a limit. Read the introduction to the Investigation on page 28 of your text.
It is important to realize that the concept of limit is a theoretical mathematical idea and that, while the real-life examples described suggest limit, they differ somewhat from a mathematical situation. Consider, for example, the graph below. Examine the graph closely before attempting the questions that follow.
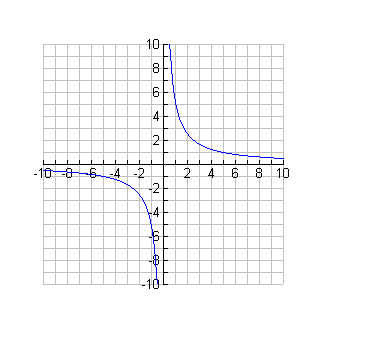
What value does y approach as x gets:
- larger and larger?
- smaller and smaller?
- closer and closer to 0?
Carry out the Investigation as outlined on pages 28 & 29 of your text. Note the explanations offered below for Steps A and D.
Step A of the Investigation requires you to imagine circles with particular sectors marked out. If you are experiencing difficulty visualizing the circles described, some models are provided for you to view.
Calculator assistance is provided should you require help with Step D of the Investigation.
Notebook Entry: Explain and illustrate a definition for "limit."
Do the Investigation Questions on pages 29 & 30 of your text. To do Investigation Question # 2, you need to look at the definition of limit in the margin of your text. For questions 5 & 6, you must look at the definitions of converging and diverging sequences in the margin.
When you have completed the investigation, you may want to look at the worked examples provided below.
Notebook Entry:Define the following terms.
- limit of a sequence
- converging sequence
- diverging sequence
Activity
C.Y.U. pages 30 - 32, #'s 7 - 21
Question #18 involves some important observations on your part. Be sure to carefully record the results.
When you have completed these questions, ask your on-site teacher to get the solutions for you from the Teacher's Resource Binder and check them against your answers. After you do this, if there is something you had trouble with and still do not understand, contact your on-line teacher for help.
Test Yourself
- A sequence that is always decreasing must converge? True or False? Explain.
- Create a sequence that has a limit of 2.
- Create a recursive sequence, other than a geometric sequence, that decreases. Determine whether or not your sequence has a limit. If so, what is the limit?
- Create a sequence that converges to 1 more quickly than the sequence{0.9, 0.99, 0.99, 0.9999, ... }.
- Does each sequence converge or diverge? If it converges, find the limit.
(a)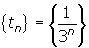 (b)
(b) 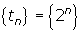 (c)
(c) 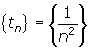
Solutions
1. False. Example: {3, 2, 1, 0, -1, -2, ...}. This series, although decreasing, does not converge.
2. There are many possible answers. Example: ![]()
3. Many answers are possible. Example: The sequence {5, 3, 1, -1, -3, ... } is a decreasing, non-geometric, recursive sequence. It has no limit since it
diverges.
4. Again, many answers exist. Example: {0.99, 0.999, 0.9999, ... }.
5. (a) Converges. The limit is o.
(b) Diverges
(c) Converges to 0.