
Learning Resources
Lesson
Carl is panning to reduce his pop intake. The purpose of this Investigation is to calculate the amount of pop he drinks by developing a formula for adding up a finite geometric series.
Read the description of Carl's pop-reduction plan outlined on page 16 of your text. You won't need to solve the posed question until the end of the procedure.
Carry out the entire Procedure to complete the Investigation. Notice that creating the sequence that describes the amount of pop he drinks is the initial step. This is a good approach to many of these problems as it lets you see exactly what it is you are dealing with.
Explanations are provided for Steps D and E. Use them only if you are experiencing difficulty.
Notebook Entry:Define the term "geometric series" in your glossary.
Begin the Investigation Questions on pages 17 &18 of your text. Clarification for questions 14 and 15 are given below.
Don't worry if you feel you don't have a clear understanding of the steps involved in this Investigation as question #13 will give you an opportunity to repeat the process. Hopefully this will serve to enhance your understanding to date.
Investigation Question #14 is where you will be deriving the general formula for finding the sum of n terms in a finite geometric series. The question generalizes the Investigation. This time, though, Wendy's amount is not half Carl's amount, but a more general r times Carl's. Once derived, copy the formula into your notebook.
Investigation Question #15: Be alert to the fact that arndoes not represent the last term of the sum, but rather the next one if the sequence were to continue. It is imperative that you have recorded the formula for adding the terms of a finite geometric series, as previously requested. This formula will be used regularly in subsequent questions. A verbal interpretation of the formula is provided.
A worked example is provided below.
Activity
Investigation Questions pages17 & 18 #'s13 - 17
C.Y.U. Page18 #'s18 - 22
When you have completed these questions, ask your on-site teacher to get the solutions for you from the Teacher's Resource Binder and check them against your answers. After you do this, if there is something you had trouble with and still do not understand, contact your on-line teacher for help.
Test Yourself
- Find the sum of the first 20 terms for each sequence below:
(a) {5, 10, 20, ...} (b) {21, 2.1, 0.21, ...} - Create a geometric series in which the initial term is 1 and the common ratio is 3. Explain why
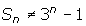 .
.
Solutions
1. (a) The sequence is geometric and has a common ratio of 2.
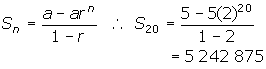
(b) The sequence is geometric with a common ratio of 0.1.
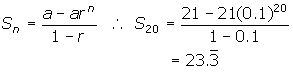
2. The sequence is {1, 3, 9, 27, ... }.
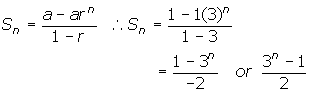
The expression given in the question was not divided by (1 - r)