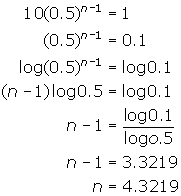Learning Resources
Lesson
The projection of population changes is one strategy a town uses to plan its municipal services. Why do you think it is important for towns to do this?
Think for a moment about the growth rate in your own town. How has it affected you, other residents, and the overall services provided? Educational reform is one topic with which you should all be familiar. Its affect on your town is, without a doubt, directly related to the projected population changes.
Read the information about the town presented in Focus C on page 14 of your text. Do not proceed any further until you have read the Focus.
Why do you suppose planners want to know when the population would double? Do you think all services would need to double if the population doubled? Is the growth rate of 0.9% per year a reasonable one? How does growth rate affect how long it takes the population to double? Discuss the answers to these questions with your classmates.
Geometric sequences can be used to describe many real-life situations, one of which is population growth. Note that t1 = 26 235 in both the explicit and recursive definitions for the sequence. This is because we are trying to write a sequence for the town's population from 1990 onward. Why is it that each term is multiplied by 1.009 to create the next term, and not 0.009? If you are unsure of the answer, create a table of populations to convince yourself that this makes perfect sense. Your table should look like the one below. You can round the populations to the nearest whole number for convenience.
Year |
Population |
1990 |
|
1991 |
|
1992 |
|
1993 |
|
1994 |
|
1995 |
|
1996 |
|
1997 |
|
1998 |
|
1999 |
|
2000 |
The completion of such a table will allow you to see that a new term is created by multiplying the previous term by 1.009.
It is imperative that you understand the difference between "percent increase" and "percent of." Although the increase in population size is 0.9%, the actual population is previous population + 0.009(previous population). This, naturally, is 1.009P. The value 0.009 is just the percent increase, not the "percent of." If this is still confusing to you, further clarification is provided.
If you require a review of geometric sequences, you may view an example before attempting the Focus Questions. If, however, you feel comfortable with the concept, proceed with the questions.
Similarly, 3 x 299 would give the 100th term. Can you figure out which term would have a value of 100 663 296? Answer.
Notebook Entry: Add the terms geometric sequence and common ratio to your glossary. Illustrations should accompany your definitions.
Some of the C.Y.U. questions involve solving exponential equations, some for which like bases cannot be found. Hence, the use of logarithms is needed. A review of this process is provided. As well, the following example shows how to use logarithms in answering questions pertaining to geometric sequences.
Activity
Focus Questions page 14 #'s 1 - 4
C.Y.U. Pages 15 & 16 #'s 5 to 12
When you have completed these questions, ask your on-site teacher to get the solutions for you from the Teacher's Resource Binder and check them against your answers. After you do this, if there is something you had trouble with and still do not understand, contact your on-line teacher for help.
Test Yourself
- Write down any two numbers and use these numbers to create two geometric sequences that satisfy the following conditions:
(a) To create the first sequence, use the first number you chose as
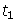and the second number you chose as 
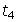.(b) To create the second sequence, use the first number as the common ratio and the second number as
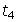. - Create two geometric sequences for each of the situations below:
(a) The first term is 6
(b) The common ratio is 0.3
(c) The eighth term is 128 - Solve for n: 10(0.5)n - 1 = 1
Solutions
1. Answers vary. Sample answers are given using the numbers 5 and 40.
(a) {5, 10, 20, 40, ... } (b) 
2. Answers vary. (a) {6, 3, 1.5, 0.75, ...}
(b) {30, 9, 2.7, ...}
(c) {1, 2, 4, 8, 16, 32,64,128, ... }
3. Divide both sides by 10 and then take the log of each side.
