
Learning Resources
Lesson
Did you have any luck discovering the "trick" Gauss used to quickly add the series? If you did, Congratulations!!! IF not, you will be able to return to the problem and solve it at the end of the Investigation.
Recall Jane's fitness program as discussed in Focus question #22 on page 9. She began by exercising 15 minutes the first day and adding 5 minutes each subsequent day. While her total walking time for the first week has been expressed using sigma notation, it has not yet been calculated. That is the purpose of this Investigation.
To be successful with the Investigation, it is important that you not be confused by the notations you will encounter. Given the sequence {![]() } = {3, 6, 9, 12, ... }. You should already know that
} = {3, 6, 9, 12, ... }. You should already know that ![]() means the first term which is 3,
means the first term which is 3,![]() represents the second term of 6,
represents the second term of 6, ![]() is the third term 9, and so forth. The sequence {
is the third term 9, and so forth. The sequence {![]() }, however, is a sequence of the sums of the terms.
}, however, is a sequence of the sums of the terms. ![]() means the sum of the first term which , of course, is just 3 (
means the sum of the first term which , of course, is just 3 (![]() itself).
itself). ![]() represents the sum of the first 2 terms which is 9,
represents the sum of the first 2 terms which is 9, ![]() is the sum of the first 3 terms which is 18, and so on. In essence, what we are finding here is the partial sums. In this case the nth partial sum, {
is the sum of the first 3 terms which is 18, and so on. In essence, what we are finding here is the partial sums. In this case the nth partial sum, {![]() }, would be {3, 9, 18, 30 ...}.
}, would be {3, 9, 18, 30 ...}.
Complete steps A and B as outlined in your text on page 11.After you have completed these two steps, you may check your workings for Step B.
Once you are assured you are on the right track, proceed with Step C of the Investigation.
Before attempting the Investigation Questions, it is essential to have a clear understanding of the outcome of the Investigation you just completed. A clarification of the formula you were to derive is provided.
Notebook Entry: Add the term "arithmetic series" to your glossary, as well as a description of the formula for finding sums of arithmetic series.
If you haven't already done so, you should now be able to solve the problem given to Gauss and his classmates. Record his strategy. You may verify your solution.
Activity
Investigation Questions page12 #'s 34 -37
C.Y.U. page 13 #'s 38 - 43
When you have completed these questions, ask your on-site teacher to get the solutions for you from the Teacher's Resource Binder and check them against your answers. After you do this, if there is something you had trouble with and still do not understand, contact your on-line teacher for help.
Test Yourself
- Given the series 1 + 3 + 5 + 7 + ... What is (a)
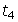 ? (b)
? (b) 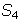 ?
? - Find the sum of the first 85 terms of each arithmetic sequence {
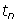 }:
}:
(a) {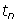 } = {7, 10, 13, 16, ... } (b)
} = {7, 10, 13, 16, ... } (b) 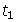 = 80
= 80 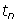 =
= 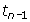 - 5, if n > 1, n ? N
- 5, if n > 1, n ? N - Find the value of the sum given by
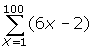
- Create an arithmetic series with 10 terms that sums to 500.
Solutions
1. (a) 7 (b) 16
2. (a) You need ![]() and
and ![]() .
. ![]() = 3n + 4, thus
= 3n + 4, thus ![]() = 259
= 259
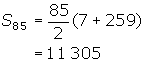
(b) The sequence is {80, 75, 70, 65 ... -340}
![]() = 85 - 5n, thus
= 85 - 5n, thus ![]() = -340
= -340
Therefore, 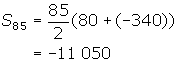
3. What you really want to find is ![]() .
.
![]() = 6(1) - 2 = 4 and
= 6(1) - 2 = 4 and ![]() = 6(100) - 2 = 598
= 6(100) - 2 = 598
Therefore, 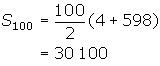
4. Answers vary. Any arithmetic series containing 10 terms where the first and last terms add to 100 will work. EX: 5 + 15 + 25 + ... + 95