Learning Resources
Lesson
This Focus introduces you to the concept of a series by adding the terms of a related sequence. The sum of the first 
terms of a sequence, 
, is called the nthpartial sum.
Consider, for example, the sequence {3, 5, 7, 9, ... }. The related series would be 3 + 5 + 7 + 9 + ... The fifth partial sum, S5, would involve the addition of the first 5 terms of the series. 3 + 5 + 7 + 9 + 11 = 35. There is a shorthand notation we can use to represent this sum. It is called "sigma notation" and involves the use of the symbol sigma, 
.
It is essential that you know how to read and understand each part of the notation. The example above can be written using sigma notation as follows: 
. The expression 2j + 1 is called the summand. Since j is the chosen variable, it is known as the index. The limits of summation are 1 and 5; 1 is the lower limit and 5 is the upper limit. You may choose to work with any variable you wish when using sigma notation. What is important however, is that you realize the variable name appears below the sigma symbol and usually also within the expression to the right of the sigma. The variable takes on the values from the first one below the sigma to the last one listed atop the sigma, increasing by 1 each time. In this example, j takes on the values from 1 to 5. In other words:
= (2 x 1 + 1) + (2 x 2 + 1) + (2 x 3 + 1) + (2 x 4 + 1) + (2 x 5 + 1)
= 3 + 5 + 7 + 9 + 11 Note: There are 5 terms to be added here
= 35
A summary of sigma notation is provided.
Do you think changing the upper and lower limits will affect the meaning of the notation? If so, how?
If you are unsure of the answer, evaluate 
.
Notice that while there are still 5 terms in the series, the lower limit is now 2 and the upper limit 6. This will now result in a sum of 45.
Can you readily tell how many terms are in a series? In the original example, the limits of summation were 1 and 5. Thus it follows that there would be 5 terms in to be added since j took on the values from 1 to 5. When we changed the limits of summation to 2 and 6, there were still 5 terms as j took on the values from 2 to 6.
What if we changed the limitsof summation to 3 and 25? How many terms would now be in the series?
The answer is not 22. Think about it; j will take on the values from 3 up to and including 25. This will give 23 terms to be added together.
Can you now tell how many terms would be summed if the limits of summation were 7 and 107?
101 is the correct answer, not 100. You should now begin to see a pattern.
In general, how many terms are summed if the sum is described as 
?
You may verify your solution.
You are now ready to proceed with Focus B and explore Jane's exercise program. After reading through the Focus, answer the related Focus Questions.
While it is essential to complete all assigned Focus Questions to ensure understanding of the concepts at hand, #22 will be referred to again in the next Investigation. Be certain you understand its solution.
Focus Question #26 is designed to help you see how to factor a scalar out of a sigma expression. For example, suppose you were to evaluate the series 
.
Your first instinct, no doubt, would be to write 5(1) + 5(2) + 5(3) + 5(4) + 5(5) + 5(6) + 5(7) and produce an answer of 140. Don't fret, this is a perfectly good approach and answer!
However, since the summand is a monomial with a factor of 5, there is a quicker way of evaluating the series. Do you know what it is? Record your thoughts and then verify your response.
Another example similar to those you will see in the Check Your Understanding section is done below.
Notebook Entry: After completing Focus B, add definitions of sigma notation, series and partial sums to your glossaries.
The great mathematician Gauss baffled his school teacher at a young age when he quickly solved a problem given him. To keep the class busy for some time, the teacher instructed them to add together all the numbers from 1 to 100. In other words, they were to add up the series below.
1 + 2 + 3 + ... + 99 + 100
Thinking this would be a tedious and time consuming task, the teacher was amazed when Gauss arrived at the answer in no time flat. Do you have any idea how he solved the problem so quickly? If not, you will have learned his "secret" by the end of the next Investigation. Meanwhile, copy the series down and try to decipher Gauss's strategy before the next lesson. If you are successful, you will have a good foundation on which to work through Investigation 1.
Activity
Focus Questions Page 9, #'s 21 - 26
C.Y.U. pages 10 & 11, #'s 27 - 33
When you have completed these questions, ask your on-site teacher to get the solutions for you from the Teacher's Resource Binder and check them against your answers. After you do this, if there is something you had trouble with and still do not understand, contact your on-line teacher for help.
Test Yourself
- Evaluate each of the following (a)
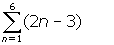(b)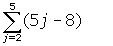 
- How many terms are summed in
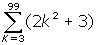? - Write the sequence {4 + 6 + 8 + 10 + ... + 50} using sigma notation.
Solutions
1. (a) -1 + 1 + 3 + 5 + 7 + 9 = 24 (b) 2 + 7 + 12 + 17 = 38
2. 97
3. The formula for the sequence is 
. You now need to find which
term is 50, to determine the upper limit of summation.
2n + 2 = 50
n = 24 Answer:
