Learning Resources
Lesson
Something to think about:
It is said that De Moivre, a mathematician whose work will come up in the final chapter, died in 1754 in an arithmetic sequence. He slept 15 minutes longer each night until he slept 24 hours and died.
In Mathematical Modeling, Book 3 you worked with sequences. Think for a moment to recall some of what you know about number sequences. Types of sequences that may be familiar to you are arithmetic, geometric and Fibonacci. Can you write an example of an arithmetic sequence? If so, put an example of one in your notebook so you will have something to refer to as some definitions are reviewed and new ones are introduced. Try to write the arithmetic sequence described in the above paragraph.
The definition of a sequence, you may recall, is an ordered arrangement of numbers, symbols, or pictures in which each item or term follows another according to a rule. Also important to note, is the fact that the domain of a sequence is the set of positive integers or the natural numbers.
Sequences may be finite or infinite. A sequence of the first 5 even natural numbers is an example of a finite sequence since it has a finite number of terms. { 2, 4, 6, 8, 10} The set of all even natural numbers, however, would produce an infinite sequence represented in the following way: {2, 4, 6, 8, 10, 12, ... } The three dots indicate that the sequence continues indefinitely according to the pattern.
Take a moment to read the opening paragraph for the chapter on page 1 of your text.
How is doubling money in an interest-paying bank account related to sequences? First of all, you need to examine how often interest is paid. How often then, does the amount of money change? Can you see that the sequence might describe the amount in month 1, month 2, month 3 and so on?
You can all think of situations in which you're sure of what will happen next because you know what happened before. For example, if today is Wednesday, then tomorrow must be Thursday. Brainstorm a few more situations.
Read the first 4 paragraphs of Focus A on page 2 of your text. Do not proceed any further until you have completed this task.
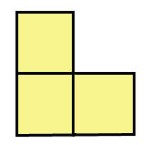
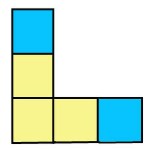
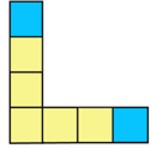
Study the T-shaped patterns below and provide a recursive description.
Standard notation is used to represent the terms of a sequence. The first term is denoted 
. The second and third terms are denoted 
and 
respectively, and so on. The nth term of the sequence is denoted 
.
As stated earlier, the domain of a sequence is the set of natural numbers. The reason for this should be quite clear now. The values of n represent the domain. It is only possible, for example, for a sequence to have a first term, a fifth term or a twentieth term. (i.e. 
). It makes no sense, for example, to refer to 
.
Sometimes a sequence is described in terms of the preceding term, 
. The initial value of the sequence can change the terms of the sequence, even if the rule relating and are the same. Thus, when writing a recursive definition, it is imperative to state the first term.
Examine the two recursive definitions below.
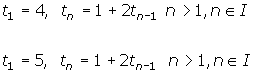
Generating the first few terms of each sequence will show that, while the rule relating the sequences are the same, they result in different terms. The terms of the first sequence are 4, 9, 19, 39, ..., while the terms of the second sequence are 5, 11, 23, 47, .... It is important to note that the only difference in the two given sequence definitions is the value of the first term. It is this value that determines the terms of the sequence.
Read the remainder of Focus A and answer the Focus questions.
An example is worked out for you below.
As you already know, the notation is used to describe the nth term of a sequence. represents the first term, the second term and so on. You must also realize that any letter, 
or u for example, can be used to describe the name of the term in the sequence. While it is the letter that is commonly used, the letters u, v and w are used on the TI-83. The calculator uses the functional format u(n), however, instead of un.
The discrete graph associated with an arithmetic sequence is a set of collinear points since the slope, the difference between consecutive terms, is constant. To graph the values of an arithmetic sequence {}, the ordered pairs (n, ) must be plotted. This can be done using the TI-83. Instructions are provided.
It is important that you keep a glossary of new terms as you proceed through this course. It will prove to be a useful tool as you work through problems and prepare for tests. It is also wise to keep them in a separate notebook.
Notebook Entry: For each of the following, include a definition, as well as a visual clue to remind yourself of what the term means.
- recursive relation
- recursion
- arithmetic sequence
- recursive formula
- common difference
- discrete graph
Activity
Focus Questions pages 3 - 5 #'s 1 to 5
C.Y.U pages 5 -7 #'s 6 to 20
When you have completed these questions, ask your on-site teacher to get the solutions for you from the Teacher's Resource Binder and check them against your answers. After you do this, if there is something you had trouble with and still do not understand, contact your on-line teacher for help.
Test Yourself
- Draw suitable diagrams to represent the recursive definition given below.
Figure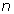
= Figure (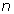- 1) + 6 squares, if 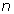> 1, ?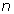 
.
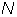- Given the sequence {5, 8, 11,14, ... }. Write a recursive and non-recursive formula to represent this sequence.
- Consider again the sequence given in #2. Determine the value of 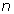for which 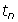= 1004.
- The modern Olympics began in 1896. can you explain why the 1988 Olympics in Seoul is referred to as the XXIV Olympiad?
- Why does an arithmetic sequence always produce linear data?
- A sequence is defined recursively as 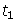= 5, 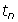= 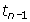+ 2, n > 1, where n ? N. Why must the restriction on n be greater than 1?
Solutions
1. Answers may vary. A sample set of diagrams is shown below.
2. Recursive definition: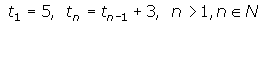 
Non-recursive definition: 
3. 1004 = 3n + 2
n = 334
4. The Olympics occur once every four years, creating an arithmetic sequence in which d = 4. Thus,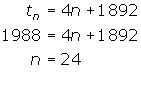 
Hence, 1988 is the 24th Olympiad.
5. The non-recursive formula which describes an arithmetic sequence is always linear, since the first level differences between the terms is constant. The slope of the line is the same as this common difference.
6. The domain of a sequence is the set of natural numbers. It is only possible to talk about the first term, second term, third term, etc. There is no such thing, for example, as the 0th term or the 1.5th term. If n was 1, you would have t0 + 2 This makes no sense. To produce terms that are reasonable, n must be an integer greater than 1.