Learning Resources
Outcomes
In this lesson you will learn
- the definition of recursion
- how to write a recursive formula for an arithmetic sequence
- how the initial term can change the terms of a sequence, even if the rule relating
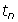and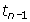 
stays the same - how to write a non-recursive (explicit) formula for an arithmetic sequence
- the relationship between the recursive and non-recursive definitions of an arithmetic sequence
- how to generate terms in an arithmetic sequence
- how to represent arithmetic sequences as ordered pairs and draw discrete graphs for them
- the relationship between the common difference of an arithmetic sequence and the slope of its discrete graph
- how to graph terms of sequences using technology
By the end of this section students will be able to :
- demonstrate an understanding of recursive formulas
- model problem situations using discrete structures such as sequences and recurrence relations
- represent arithmetic and geometric sequences as ordered pairs and discrete graphs
- represent a series in expanded form and using sigma notation
- develop, analyze and apply algorithms to generate terms in a sequence
- develop, analyze and apply algorithms to determine the sum of a series
- demonstrate an understanding for recursive formulas, and how recursive formulas relate to a variety of sequences
Introduction
As its name suggests, this section introduces the definition of recursion in the context of sequences. You will explore arithmetic sequences, not only algebraically , but visually as well. This should enable you to see the relationship between recursive and non-recursive formulas.
Be alert to patterns in the sequences presented, as it is the comparison of these patterns that will help you make sense of recursive and non-recursive formulas.
As well, in this section you will plot discrete graphs of sequences and develop a formula for adding finite arithmetic series.
Everyone is familiar with the song "The Twelve Days of Christmas." Did you ever wonder just how many gifts, in total, the sweetheart received from her true love? You will have an opportunity to solve this in the Challenge Yourself question at then end of the first section.
It should take approximately 4.5 hours to complete this section of study.
Prerequisites
To be successful in this lesson, it would be helpful to know the following:
- what is meant by a discrete graph
- the definition of a sequence
- the definition of an arithmetic sequence and readily give examples of such
- what is meant by the phrase "common difference" as it relates to arithmetic sequences
- the concept of n! (for question #12)