
Learning Resources
Lesson
This Focus takes the pattern developed in Focus J and generalized it for any situation.
The following reasoning applies:
- Suppose you have n trials of an experiment in P(Success) for each trial is p. You want to determine the probability of obtaining exactly r successes. This variable is called a random variable since it can take any value in the sample space.
- There are nCr ways of getting r successes out of n trials.
- Since the P(Success) = p, then the probability of getting r successes will be pr .
- Getting r successes can be described as obtaining r successes and the rest are failures. Since there are r successes in n trials, then there must be (n - r) failures. Since the probability of failure is the complement of the probability of a success we have P(failure) = P(success) = (1 - p). The probability of obtaining (n - r) is given by (1 - p)n - r .
- This results in the overall probability as
![]()
This function is widely used to analyze binomial experiments. Graphing calculators and spreadsheets have built in functions for determining probabilities in binomial experiments.
Example
A survey of university of students indicated 75% of the students preferred coffee over tea. If a random sample of 25 students is taken one month later, what is the probability that 20 of them prefer coffee?
Solution
There are 25C20 ways of selecting 20 students out of 25
For each student we have the following probabilities:
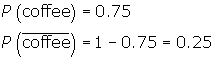
By the theoretical model, the overall probability will be
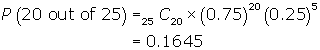
You should now be ready to complete the assigned work on this lesson.
Activity
Check Your Understanding p.349 - 350. Complete 12 to 20 inclusive
When you have completed these questions, ask your on-site teacher to get the solutions for you from the Teacher's Resource Binder and check them against your answers. After you do this, if there is something you had trouble with and still do not understand, contact your on-line teacher for help.
Test Yourself
- A fair die is rolled six times. Find the probability of rolling exactly 3 sixes.
- In the example from the lesson, explain how to find and find the probability of 20 or more students preferring coffee.
Click here for a suggested solution.