
Learning Resources
Lesson
Investigation 14
In this investigation you will explore the relationship of Pascal's Triangle to the expansion of the expression (x + 1)n. To see this relationship you need to write the expansion of (x + 1)n for values of n from at least 0 to 4. This is done in a step by step approach below so you can see how the power was expanded.
You should complete at least the expansion for the power of 5 as required in Investigation 14 on page 342. Note that the power of the binomial corresponds to the row number of Pascal's Triangle. Thus row n of Pascal's Triangle should give the coefficients of (x + 1)n .
Focus I
We now want to extend what we discovered about the coefficients of (x + 1)n to the expansion of all binomials. We will look at (x + y)n and then use what we discover to expand binomials like (2x + 3y)5. However, let's first review what we discovered about (x + 1)n as it relates to Pascal's Triangle and extend that to combinations.
We learned that the coefficients of the expanded form of (x + 1)n are the elements of row n of Pascal's Triangle. In an earlier lesson we learned that the elements in row n of Pascal's Triangle are the combinations nC0 , nC1, nC2 , nC3 , nC4 , etc. Thus we can write:
(x + 1)n =nC0 xn + nC1 xn-1 + nC2 xn-2 + ...+ nCn-2 x2 + nCn-1 x + nCn 1
The above expression looks more complicated than it is. When it is written for a specific value of n it becomes more familiar. For example, if n = 4 we have:
(x + 1)4 =4C0 x4 + 4C1 x3 + 4C2 x2 + 4C3x + 4C41
(recall that nC0 and nCn are both equal to 1).
The coefficients of the expansion of (x + y)n have exactly the same relation to the elements of Pascal's Triangle as does the coefficients of the expansion of
(x + 1)n . However, we need to take a look at the exponents of the variables x and y in each of the terms of the expanded version. This is best seen by working through a few examples.
Note the exponents on the two variables. The exponent for the first variable starts at n, the exponent to which the binomial is raised, and decreases in each successive term by 1 till it reaches 0. The exponent for the second variable starts at zero (y0 = 1) in the first term and increases by 1 in each successive term till it reaches n.
Note also the coefficients of each of the terms in the expanded form are the elements in the corresponding row of Pascal's Triangle which can be found using combinations. Thus the coefficients may be written using combination notation similar to what was used above for (x + 1)n .
Let's apply this to the expansion of a binomial to a higher power.
Example 1
Write the first 4 terms of the expansion of (x + y)9 .
Solution
We know that the coefficient of the first term of the expansion is 1 and the coefficient of the second term is 9. The coefficient of the third term is 9C2 and of the fourth term is 9C3. These are evaluated below:
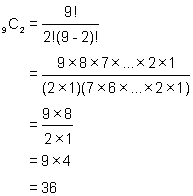
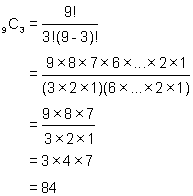
It is now a matter of using the pattern for the exponents of the variables to write the first four terms of the expanded form.
(x + y)9 = 1x9 + 9x8y +36x7y2 + 84x6y3 + ........
Notice that the exponent of x starts at 9 and decreases while the exponent of y starts at 0 (and hence is not written down) and increases.
We now want to replace x and y in the binomial by other terms. The pattern of exponents and coefficients remain the same. We just have to be careful what term or expression we are raising to what power.
Example 2
Use your knowledge of Pascal's Triangle and combinations to expand the binomial (2a + 3b)6.
Solution
Think of (2a + 3b)6 as (x + y)6 with x = 2a and y = 3b. The expansion, written using combination notation is:
(2a + 3b)6 = 6C0(2a)6 + 6C1(2a)5(3b) + 6C2(2a)4(3b)2 + 6C3(2a)3(3b)3 +
6C4(2a)2(3b)4 + 6C5(2a)(3b)5 + 6C6(3b)6
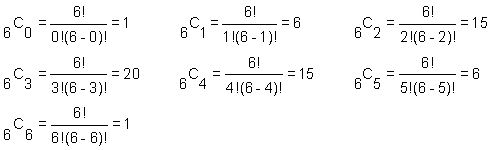
If you have a copy of Pascal's Triangle to row 6 recorded in you note book, these values could have been read directly from there without having to do the calculations. Either way we have:
(2a + 3b)6 = 1(2a)6 + 6(2a)5(3b) + 15(2a)4(3b)2 + 20(2a)3(3b)3 +
15(2a)2(3b)4 + 6(2a)(3b)5 + 1(3b)6
Now simplify each of the terms (e.g. (2a)6 = (2a)(2a)(2a)(2a)(2a)(2a) = 64a6. This gives:
(2a + 3b)6 = 64a6 + 576a5b + 2160a4b2 + 4320a3b3 + 4860a2b4 + 2916ab5 + 729b6
The two examples suggest an algorithmic method for expanding ![]() . Using
. Using ![]() as an example follow the steps:
as an example follow the steps:
First, write the terms without the coefficients. Start with the highest power of a and with the exponent of b = 0. The sum of the exponents is 5. Write subsequent terms with decreasing values of the exponent for a and increasing values for the exponent of b .
![]()
Each term is formed by combinations of the a and b terms. The combinations are ![]() . Fill these in for the placeholders
. Fill these in for the placeholders
![]()
Evaluate the combinations and simplify the expression as much as possible.
Activity
Investigation Questions p.343. Complete 9 and 10
Check Your Understanding p.343. Complete 11, 12, 13 and 14
Focus Questions p.344. Complete 15 and 16
Check Your Understanding p.345. Complete 17 to 22 inclusive
When you have completed these questions, ask your on-site teacher to get the solutions for you from the Teacher's Resource Binder and check them against your answers. After you do this, if there is something you had trouble with and still do not understand, contact your on-line teacher for help.
Test Yourself
1. Use your knowledge of Pascal's Triangle to write the first four terms of (x 1)15 .
2. Use combinations to expand the expression (3x - 2)5.
Click here for suggested solution.