Learning Resources
Lesson
Pascal's Triangle is named for a French mathematician Blaise Pascal, even though it had been known for centuries. The analysis of the patterns found within the triangular array of numbers and its usage can be credited to Pascal.
Investigation 12
Pascal's Triangle is a triangular array of numbers that has many patterns imbedded within it. In this investigation we will look at only a few of these.
For Step A, the main pattern in which we are interested is the one we will use to construct the "triangle". This pattern is that "any element in the triangle is the sum of the two elements above it , immediately to the left and to the right". Copy the triangle from your textbook and extend it to al least 10 rows. To help you to do this, ask your on site teacher to get you Blackline Master 5.5.1 from the Teacher's Resource Binder. Fill it in and place it in your notebook. Determine the number in each cell in the 2nd row by applying the pattern stated above and in your textbook. After you figure out what the number should be, click on each ? mark in the triangle below to check your answer. Then repeat the same for row 3, 4, etc.
|
Row 0 1 2 3 4 5 6 7 |
Step B asks you to find "as many patterns as you can" in the triangle. One possibility you might consider is to investigate the diagonals. Use the above diagram, reset everything to ? marks and then highlight the first diagonal. Is there a pattern? Repeat the process and highlight the second diagonal. What pattern does this show? What about the other diagonals? There are many other patterns. Find as many as possible and do some research on Pascal's Triangle and its place in mathematics.
For Step C, share what you find with the other members of your class (either on site or via the net). See if you can find a pattern that your friends did not see.
Investigation 13
Before beginning this investigation, recall that to evaluate combinations the formula uses factorials. Two special factorials to make note off are 1!, which is obviously 1, and 0!. Mathematicians have defined 0! as 1 as seen earlier. Note that this is a definition and no proof of it is required or possible.
In Step A, read the note in the sidebar before doing the calculations. Again in this investigation use Blackline Master 5.5.1 to enter your calculations. Define the top row as row zero as in the previous investigation. For example the second element in the row 4 is given by 
. Note the first number gives you the row of Pascal's Triangle and the second number is one less than the element of that row - the athelement in the nthrow is found by using 
. For example to find the 5th element in the 12th row you would calculate 
.
Let's calculate a combination and compare it to the number in Pascal's triangle.
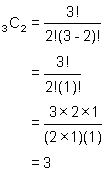
Use the triangle and go to row 3. Click on element number 3 in this row. What is the value? How does it compare to 3C2?
Lets try another combination.
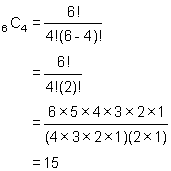
Use the triangle above and go to row 6. Click on element number 5 in this row. What is the value? How does it compare to 6C4?
For Step B, you should see the relationship between these combinations and Pascal's Triangle. Make a conjecture. Evaluate nC r for several other values of n and r and use the triangle to check your conjecture.
The relationship between the elements of Pascal's Triangle and combinations is summarized below.
The elements in Pascal's Triangle follow the pattern shown below when they are written using combinations:
|
Row 0 1 2 3 4 |
This information gives a convenient pattern for finding any element of the triangle without completing the table up to the row containing the required element. This will be of advantage to us in the next lesson dealing with the expansion of binomials.
Example
Find the fourth element in row twelve of Pascal's Triangle.
Solution
To find this value evaluate 
since the athelement in the nthrow is found by using .
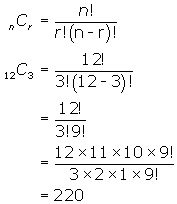
You should now be ready to complete the assigned work on this lesson.
Activity
Check Your Understanding p.340. Complete 1 and 2
Investigation 13 Questions p.341. Complete 3
Check Your Understanding p.341 - 342. Complete 4, 5, 6, 7 and 8
When you have completed these questions, ask your on-site teacher to get the solutions for you from the Teacher's Resource Binder and check them against your answers. After you do this, if there is something you had trouble with and still do not understand, contact your on-line teacher for help.
After you do the assigned activities, continue on to the Test Yourself section below for a quick quiz on this lesson.
Test Yourself
Use combinations to find the following elements in Pascal's Triangle:
- The first three elements in row 9.
- The 7th element in row 10.
Click here for suggested solution.