
Learning Resources
Lesson
We now focus again on calculating probability. Recall that for an event X, the probability of X occurring is given by the formula:
![]()
Read and study the examples given in your textbook; discuss these with your classmates and/or teacher. You will note that in example 8, for both cases there is only one favourable outcome, so the numerator is 1.
Note for example 9 the nine people include six males and three females. There is more than one favourable outcome. Hence the numerator will not be 1. In part (a) of example 9, the question can be translated as "What is the probability of randomly choosing five males?". Since there are more than five males, there is more than one favourable outcome. There are 6C5 ways of choosing five people from a group of six. This number represents the number of favourable outcomes. Five people are chosen from a group of nine, so there are 9C5 ways of choosing the five people. The probability is given by
![]()
At first glance, part (b) of example 9 might look like part (a) to you. There is one important difference: in part (b) the total number of males chosen is smaller than the total size of the group. This means that some females will be chosen. You must therefore account for the fact that the group of females can be chosen in several ways. To count the favourable outcomes you must realize that to choose 3 males you must choose 2 females to complete the group of 5. There are 6C3 ways of choosing the three males from a group of six and there are 3C2 ways of choosing two females from a group of three. According the Multiplication Principle the number of favourable outcomes is given by 6C3 x 3C2 . The total number of outcomes is given by 9C5
In the following examples the "total number of possible outcomes" and sometimes the "number of ways of X occurring" involve calculating combinations, permutations and/or the Fundamental counting principle.
You should be familiar with the concepts of probability, and you should also be comfortable working with combinations and permutations. This is best shown by working through some examples.
Example 1
A regular deck of 52 playing cards is well shuffled. You are dealt 5 cards. What is the probability you receive three aces and two eights?
In the above example, both the number of ways that event X could occur and the total number of outcomes were combinations. It some examples one or both of these could be permutations. Consider the following example.
Example 2
The security system on a building has a 4 digit code that must be entered to deactivate the alarm when the door is first opened in the morning. The pad on which the code is to be entered contains the10 digits 0 through 9. What is the probability that a thief could randomly enter the correct code and deactivate the alarm if (1) no digit is allowed to be used more than once in the code, (2) digits are allowed to be repeated in the code.
Solution
(1) There is only one correct code, hence the number of outcomes which favour event X is 1. The total of all possible outcomes is a permutation of the 4 digits chosen from a set of 10, i.e. 10P4, which from the formula is:
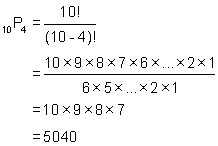
Thus the probability of randomly deactivating the alarm is ![]()
(2) Again there is only one correct code so the number of outcomes which favour event X is 1. The total of all possible outcomes can be found by using the multiplication principle. Since repetition is allowed, there are 10 different choices for each digit. Thus the total number of all possible outcomes is:
10 x 10 x 10 x 10 = 10000
Thus the probability of randomly deactivating the alarm is ![]()
Activity
Focus Questions p.337. Complete number 1
Think About p.339
Check Your Understanding p.337 - 339. Complete 2 to 15 inclusive
When you have completed these questions, ask your on-site teacher to get the solutions for you from the Teacher's Resource Binder and check them against your answers. After you do this, if there is something you had trouble with and still do not understand, contact your on-line teacher for help.
Test Yourself
A local group is raising funds to send the school team to a national tournament. They devise a lottery, similar to 6/49, that requires you to choose 4 numbers from 1 to 20. If you buy one ticket, what is the probability of winning this lottery?
Click here for a suggested solution.