
Learning Resources
Lesson
We now wish to develop a formula for calculating the "the number of combinations of n items taken r at a time" or "n choose r". The mathematical notation for this English expression is nC r .
Recall from our first lesson in this section that a permutation is an arrangement of a set of things in a particular order and that a combination is an arrangement of a set of things without regard to order.
The formula for nC r is best explained by the use of a simple example.
Consider choosing sets of 3 letters from the 5 letter set A, B, C, D, E. If order matters ( e.g. ABC is considered different than ACB), then we are dealing with permutations and we know the number of "different" sets is:
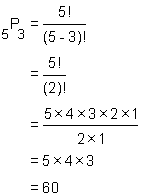
Consider closely the 3 letter set ABC. This set yielded the following permutations: ABC, ACB, BAC, BCA, CAB, CBA. This is 6 or 3! different permutations. However, each of these sets of 3 are the same combination. We have 6 or 3! permutations but only 1 combination of the same three elements from the set. The number of permutations is 6 or 3! times larger than the number of combinations.
Similarly, any other 3 letter set taken from the set of 5 will yield 3! permutations but only 1 combination. Thus, in this example, the number of permutations is 6 or 3! times larger than the number of combinations. Thus we can get the number of different combinations by dividing the number of permutations by 3!. We can say that:
![]()
This is "the number of combinations of 5 items taken 3 at a time". If we extend this pattern to "the number of combinations of n items taken r at a time" or nCr we get:
![]()
Replace nPr by the expression we obtained in the last lesson and state the formula for nC r totally in terms of factorials.
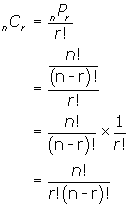
Formula for Calculating Combinations
In general, we can say that "the number of combinations of n items taken r at a time" or "n choose r" is given by the formula:
![]()
Although it helps understanding when you know how a formula is derived, the main outcome desired in this section is to be able to use the formula in problem solving situations. To do this you have to be able to distinguish between situations which require counting permutations and those which require counting combinations. Remember these formulae are nothing more than a means of counting.
Example
A group of three people are to be chosen at random from your class to respond to a questionnaire about youth facilities in your community. If there are 17 in your class, how many different ways can the group be chosen?
Solution
Since order is not important, the group is a combination. We are choosing a combination of 3 from a group of 17. This is 17C3 and is calculated as:
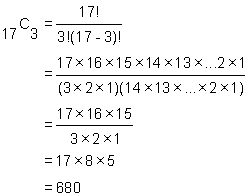
You should now be ready to do the work assigned for this lesson; remember that the exercises include problems that require both permutations and combinations, you have to decide which is applicable.. Go to the top of the page an click on the Activities button.
Both nPr and nCr can be calculated using the TI-83. To see the key strokes necessary for nPr press here. The keystrokes necessary for nCr are identical, except you select nCr instead of nPr on the probability sub-menu.
Activity
Check Your Understanding p.333 - 334. Complete 21 to 34 inclusive.
When you have completed these questions, ask your on-site teacher to get the solutions for you from the Teacher's Resource Binder and check them against your answers. After you do this, if there is something you had trouble with and still do not understand, contact your on-line teacher for help.
After you do the assigned activities, continue on to the Test Yourself section below for a quick quiz on this lesson.
Test Yourself
In a tennis tournament, $150 000 is to be distributed in prize money. The tournament has 16 players and the money is to be divided among the top 4 finishers. In how many ways can the money be distributed if:
- Each of the top 4 players receives $37 500?
- The 1st place player gets $80 000, the 2nd place player gets $40 000, the 3rd place player gets $20 000, and the 4th place player gets $10 000?
Click here for a suggested solution.