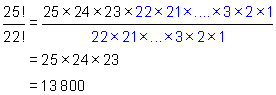Learning Resources
Lesson
We said in an earlier lesson that to calculate theoretical probability we have to count two things: the total number of possible outcomes and the number of ways a given event X can occur. This lesson deals with how to count the number of permutations and combinations of a given set of objects.
Let's begin by first defining what each of the terms mean. Then we will then turn our attention to counting them.
Permutation: A permutation is an arrangement of a set of things in a particular order.
Suppose the set is the letters P, Q , R. If we consider all three elements of the set, the permutations are: PQR, PRQ, RPQ, RQP, QPR, QRP. The order of the letters matter. Each arrangement is a different permutation of the original set. There are 6 different permutations in all. You can think of this has having 3 choices for the first letter, 2 choices for the second and only 1 for the third; therefore, by the fundamental counting principle the number of possible arrangements would be 3 x 2 x 1 = 6.
We could also select only 2 of the 3 elements from the set P, Q, R and consider the different permutations of these. The different permutations of two elements from this set would be: PQ, QP, PR, RP, RQ, QR. Again order matters. Each arrangement is a different permutation of 2 elements of the 3 in the set. There are 6 different permutations in all. Again you can think of this has having three choices for the first letter and 2 choices for the second letter resulting in 3 x 2 = 6 arrangements.
Combination: A combination is an arrangement of a set of things without regard to order.
Consider the second situation above: select 2 of the 3 elements of the set P, Q, R and determine the different combinations of these. Since a combination does not regard order, the arrangements PQ and QP are the same combination. Similarly PR and RP are the same combination, and RQ and QR are the same combination. There are only 3 different combinations of 2 things taken from a set of 3.
Investigation 10 on page 327 in your text deals with permutations and combinations. If you have difficulty with it, some hints and directions are given below.
Investigation 10
Step A deals with combinations. You should check with your classmates (either on site or via the net) to ensure that you have all the required combinations before you go on to Step B. (Hint: you should have 10 of them). Be systematic in the way you make your listing and you should obtain all of them.
Step B involves permutations. There is a lot more arrangements here than in Step A. Organize you work to have a systematic approach to the listing and share the work with a classmate. For example, you could list all the permutations involving A and your classmates permutations that don't involve A.
Hint: Instead of listing all the possibilities , can you count them without listing? How many ways can the highest mark be assigned? Once the highest mark has been assigned, how many ways are left to assign the second highest mark? The third highest? Check the interactive window below for an analysis of this.
For Step C make sure to record in your notebooks the response to this question. It is answered on the first page of this lesson. You need to record it for future reference.
Focus F
Before we consider how to count/calculate the number of permutations on a given set, we have to consider a new notation that will be of immense benefit in these calculations. This new notation is introduced by means of the following example.
Example 1
Suppose there are 10 people in your Mathematics 3205 class who write a unit test. Also, suppose each receives a different score on the test. In how many different ways could the 10 scores have been distributed among the 10 students?
Solution
From our work on Investigation 10 we can reason as follows: There are 10 different people who could have received the highest mark. That leaves 9 different people who could have received the second highest mark. Similarly, there are 8 who could receive the third highest mark, and so on.
By the Fundamental Counting Principle, the total number of ways the 10 marks could have been distributed to the 10 people are:
10 x 9 x 8 x 7 x 6 x 5 x 4 x 3 x 2 x 1
This is a very large number (3 628 800 to be exact). In fact, the product of successive integers starting at a certain integer and continuing down to 1 gets unwieldy very quickly (try 15 x 14 x 13 x ....x 3 x 2 x 1 and you will see for yourself).
To write such an expression every time we have to deal with a similar type of problem would be a pain. However, mathematicians have solved that problem for us. They invented a notation that would represent that product without actually writing it all out. To express the first product above, 10 X 9 X ...X 2 x 1, we simply have to write 10!. Similarly, to express 15 X 14 X 13 X ...X 2 x 1, we write 15!.
The "!" symbol is not read as in English. In mathematics, we do not say "10 exclamation mark". In mathematics we read it as "10 factorial".
Factorial: The product of all positive integers equal to and less than a given
positive integer. The notation for it is n!, and this is read as "n
factorial". Thus:
n! = n x (n - 1) x (n - 2) x (n - 3) x ... x 3 x 2 x 1
This notation will be very beneficial in the rest of our work on permutations and combinations. Some examples of its use are shown below:
Example 2
Compute ![]()
Solution
Example 3
Simplify: ![]()
Solution
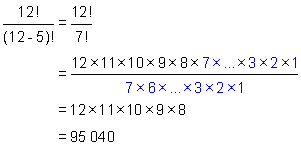
Example 4
Evaluate ![]()
Solution
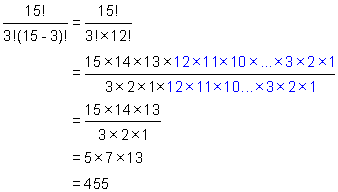
You should now be ready to do the work assigned for this lesson.
Activity
Investigation Questions p.328. Complete 1 and 2.
Think About p.328, p. 329 and p.330
Check Your Understanding p. 328. Complete 3 to 7 inclusive.
Check Your Understanding p. 330. Complete8 to 14 inclusive
When you have completed these questions, ask your on-site teacher to get the solutions for you from the Teacher's Resource Binder and check them against your answers. After you do this, if there is something you had trouble with and still do not understand, contact your on-line teacher for help.
Test Yourself
Identify each of the following as an example of a permutation or a combination.
- Picking two names from a hat to receive a prize of $50 each.
- Picking two names from a hat, the first to receive a prize of $50 and the second a prize of $25.
- Picking six numbers for the Loto 649 draw.
- Picking which three horses will be leading at the end of an 8 horse race.
- Picking which horse will finish first, which horse will finish second, and which horse will finish third in an 8 horse race.
Click here for suggested solution.