Learning Resources
Lesson
Focus E
Read and study the example in this Focus regarding conditional probability; the example can be worked through without too much difficulty.
When events are independent, the outcome of one event is not affected by the outcome of another. Mathematically, you seen this earlier as
.
For example, when two cards are drawn from a deck of cards, with the first replaced before the second is chosen, the results are independent. If the card is not replaced, then the second choice is affected since there will be only 51 cards left to draw from.
If event B depends upon or is conditional on, the occurrence of event A , then the events are dependent. The probability of event B occurring when event A has already occurred is represented by 
and is read as "the probability of event B occurring given that event A has occurred" . This is called conditional probability .
In terms of Venn diagrams, you can view the interpretation in the interactive window by stepping through it.
From this demonstration we can conclude that
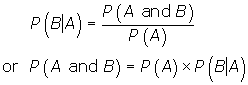
Example 1:
If two cards are drawn from a regular 52-card deck and the first is not replaced before the second card is drawn, what is the probability of drawing 2 Aces? 2 spades?
Solution:
(a) Let A represent the event "choosing an Ace on the first draw" and B represent "choosing an Ace on the second draw" .
If an Ace is obtained on the first draw, there are 3 Aces left in the remaining 51 cards giving
Therefore,
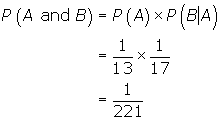
The probability of selecting 2 Aces is 
(b) Let X represent the event "choosing a Spade on the first draw" and Y represent "choosing a Spade on the second draw" .
If a Spade is obtained on the first draw, there are 12 Spades left in the remaining 51 cards giving
Therefore,
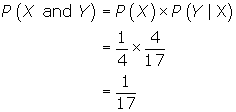
The probability of selecting 2 Spades is 
Complete the Focus questions and first set of Check Your Understanding in the Activities Section before continuing.
Investigation 8
In this activity the relationship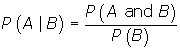 
is further investigated by using tree diagrams.
Steps A and B are intended for you to see how you can use a tree diagram to find the number of favourable outcomes for an event and the total number of outcomes. Step A simply asks you to enter the values from the table into the appropriate boxes and Step B to write in the probabilities in a tree diagram.. Complete each tree as requested.
Step C is a probability tree diagram. Do you see any patterns? Consider P(pass/graduated), P(pass and graduated) and P(graduated). How are they related?
Example 2:
An engineer calculates that, for a one-year period, the probability of failure is 0.65 for a brake rotor and 0.40 for a brake pad.
- Represent the information using a tree diagram
- Calculate the probability that, for a randomly chosen brake assembly, the rotor will will fail and the pad will not.
Solution:
Step through the following interactive window to view the construction of the tree diagram.
Complete the Investigation questions and Check Your Understanding in the Activities Section.
Activity
Focus Question p.320, Complete 46
Check Your Understanding p.320 - 321, Complete 47, 48, 49,50 and 51
Investigation Questions p.323 - 324, Complete 52, 53, 54, 55, 56 and 57
Check Your Understanding p.324, Complete 58, 59 and 60
When you have completed these questions, ask your on-site teacher to get the solutions for you from the Teacher's Resource Binder and check them against your answers. After you do this, if there is something you had trouble with and still do not understand, contact your on-line teacher for help.
After you do the assigned activities, continue on to the Test Yourself section below for a quick quiz on this lesson.
Test Yourself
In a Level III class of 30 students, each students registers for M3204 or M3205 and one science, either Physics 3204 or Chemistry 3202. The choices are given in the table below:
Physics 3204 |
Chemistry 3202 |
Total |
|
M3205 |
4 |
3 |
7 |
M3204 |
13 |
10 |
23 |
Total |
17 |
13 |
30 |
Assume that event B is "registers for M3205" and event A is "registers for Physics 3204". Write each of the following probabilities with the proper notation:
- What is the probability of selecting a student at random who registers for both M3205 and Physics 3204?
- What is the probability of selecting at random a student registering for M3205 who is also registering for Physics 3204? who is also registering for Chemistry 3202?
- What is the probability of selecting a student at random who registers for Chemistry 3202 and who is also registering for M3204?
- Use a tree diagram to summarize the choices for the students in this class.
Click here for a suggested solution.