
Learning Resources
Lesson
For the purpose of this lesson we will refer back to Question 14 on page 305 in your text. That problem stated:
"Andrew has to ride the bus to the DMV building to take the written driver's test. He can use either Route 3 bus which passes by the bus stop every 20 min or Route 5 bus which passes by the same bus stop every 15 min. It is raining and he will get soaked if he has to wait for more than 5 min. What is the probability he will not get soaked?"
When you did the above question on page 305, you calculated the experimental probability that Andrew would not get wet. We now want to calculate the theoretical probability for the same events.
Let event A be "Route 3 bus arrives within the 5 min wait" and let event B be "Route 5 bus arrives within the 5 min wait". We wish to calculate P(A or B) as this is the probability Andrew will not get soaked (i.e. the bus picks him up in time).
Since Andrew can wait only 5 min and since Route 3 bus arrives every 20 min we have:
![]()
Also since Route 5 bus arrives every 15 min we have:
![]()
Events A and B are not mutually exclusive as both buses could arrive at the same time. We have to determine P(A and B) so we can use the Addition Principal to calculate P(A or B).
One method of doing this is to use an area model to represent the two events. The total area involved will measure 20 by 15. This represents all the total possible waiting times. On grid paper mark off a rectangle with these dimensions as shown below.
Route 5 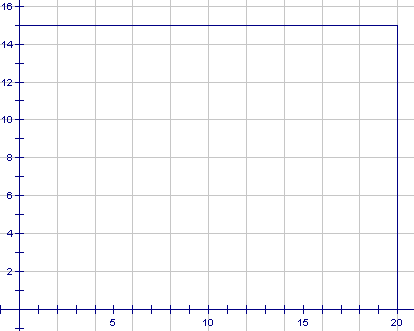
Route 3
Now shade an area to represent Event A, "Route 3 bus arrives within the 5 min wait". This will be a rectangle 5 units wide along the Route 3 axis stretching the length of the Route 5 axis. It is shown below:
Route 5 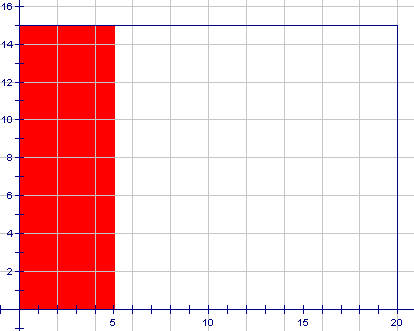
Route 3
Next shade an area to represent Event B, "Route 5 bus arrives within the 5 min wait". This will be a rectangle 5 units wide along the Route 5 axis stretching the length of the Route 3 axis. It is shown below:
Route 5 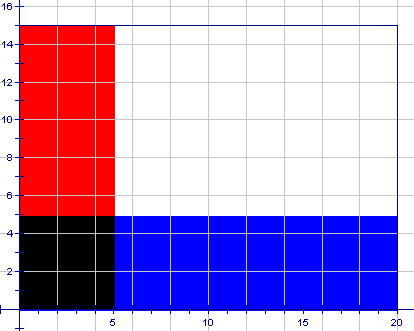
Route 3
The total area representing "all possible outcomes" is 20 by 15 or 300 square units. The black area which represents "Event A and Event B happening" is
5 by 5 or 25 square units. Thus:
![]()
We can now solve the original problem:
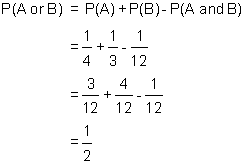
An alternate to using the Addition Principle would be to calculate P(A or B) directly from the area diagram. To do this note that the total un-shaded area is 10 by 15 or 150 square units. Thus the total shaded area is the total area minus the un-shaded area, 300 - 150, or also 150 square units. Thus:
![]()
Either way, the answer is the same.
We will apply an area model to the "Meeting Problem" that we did in Investigation 2 on page 304 of your text.
The "Meeting Problem" of Investigation 2 stated:
"Alyssa and Ja-Wen are scheduled to take their written tests on the same morning. They agree to arrive outside the DMV building between 10:00 and 10:30 a.m. Neither plans to spend more than 10 min waiting for the other. What is the probability they will meet?"
In Investigation 2 you ran a simulation of this problem and calculated an experimental probability. We now wish to calculate the theoretical probability for this same problem. To do it we will construct an area model and use it to calculate the probability. Because this problem may cause some difficulty for you, it is presented in a step by step fashion below. Simply click on start to begin
Activity
Focus Questions p.316 - 317. Complete 37, 38, 39 and 40
Check Your Understanding p.318 - 319. Complete 41 to 45 inclusive
When you have completed these questions, ask your on-site teacher to get the solutions for you from the Teacher's Resource Binder and check them against your answers. After you do this, if there is something you had trouble with and still do not understand, contact your on-line teacher for help.
Test Yourself
Your basketball team is trailing by one point. Just at the buzzer to end the game you are fouled and are awarded two free throws. From past experience you know that the probability you will make any free throw is 60%. What is the probability you will:
- Win the game?
- Tie the game?
- Lose the game?
Click here for suggested solutions.