
Learning Resources
Lesson
These investigations assumes that you are familiar with Venn diagrams; review the note in the sidebar of your text book. If you are still having problems seek help from your online teacher. These two investigations and focus will use Venn diagrams to explore probabilities.
Investigation 5
In this investigation a Venn diagram is given to represent a situation and you have to interpret it through the various steps in the procedure. Step A and Step B may seem to be very similar; however, there is an overlapping region which means you must distinguish between the number who own a car only and the number who own a car will include those that also own a truck.
For Step C the word "and" implies a shared or overlapping region on the Venn diagram. In Step D, the "or" implies all of the regions that are mentioned. This is not the same as adding the number of people who own a car and the number of people who own a truck since there some people who own both. The value will be the sum of those who own a car only, own a truck only and who own both.
For Step E, the quantity is represented by the sum of the numbers not in the "own a truck" region.
It is important in the investigation questions that you not become confused with the work done in the previous lesson. Notice that the word outcome is used to avoid confusion with the term event. There are two items of interest - a car and a truck -but only one event and that is "what does the person own".
Complete investigation 5 questions before continuing.
The main point to remember is that we are looking at Venn Diagrams primarily as a tool for counting.
Example 1
In a survey of home technology, out of 100 households asked, 70 said they had a computer, 35 had a DVD player, and 10 had both in their home. Draw a Venn Diagram to represent this information.
Solution
In the above example, suppose we let "own a computer" be event A and "own a DVD player" be event B. Let's use the Venn Diagram to help calculate some probabilities associated with these two events.
![]()
![]()
![]()
![]()
From the given information , the last probability, P(A or B), is not obvious . We need to refer to the Venn Diagram to get a count of the number that satisfies the condition A or B. The temptation is to try to calculate P(A or B) by adding P(A) to P(B). Doing that for this example we get:
![]()
Clearly this is different than P(A or B) calculated above and in fact is impossible since any probability cannot be greater than 1. Thus we can say for the above example that:
![]()
But could there be events A and B such that P(A or B) = P(A) + P(B)? That possibility is explored in Investigation 6.
Investigation 6
In the first investigation of this lesson you explored events which could be described as not mutually exclusive since there was overlap in the events. In this investigation you will explore what happens with probabilities when the events have no overlap or are described as mutually exclusive events. As the definition in the sidebar of your text (p.313) points these are events that do not occur together.
The steps in this procedure are straightforward and should pose no problems for you. Make sure to interpret each in terms of the Venn diagram.
Example 2
In a survey of 100 people, it was found that 10 were over-weight and 2 were under-weight. Draw a Venn Diagram to represent this information.
Solution
Since a person cannot belong to both groups, it is clear that the two areas of the Venn Diagram representing them do not overlap.
In the above example, suppose we let "is over-weight" be event A and "is under-weight" be event B. Let's use the Venn Diagram to help calculate some probabilities associated with these two events.
![]()
![]()
![]()
![]()
We refer to the Venn Diagram to get a count of the number that satisfies the condition A or B and the condition A and B. In this situation, if we calculate the P(A or B) by adding P(A) to P(B) we get:
![]()
For this situation, this is the same as P(A or B) calculated above.
So when can we add P(A) to P(B) to get P(A or B)?
The answer can be seen by close inspection of the Venn Diagrams. If there is no overlap of the two events (that is if the two events cannot occur together), as in the second example, we can add the probabilities to get P(A or B). Such events are called mutually exclusive events because the occurrence of one excludes the occurrence of the other.
Complete investigation 6 questions before continuing.
Focus C
Read and study the material found in this Focus; however note that there is an error in your text book on page 314. The book gives:
![]()
It should be:
![]()
As well make note of the following points regarding the Venn diagram given:
- Region A includes all those who passed the driving test in one attempt
- Region B includes all those who graduated from driver training
- The portion of the diagram that is shared between A and B includes those who fulfilled both requirements; that is, those who graduated from driver education and who passed the test in the first try.
- The region within either oval denotes "A or B". Note that if you added the probabilities of P(A) and P(B) then you count P(A and B) twice (unless the events were mutually exclusive)
- If you add the probabilities, they do not add to 1; the remaining amount is outside "passed in one try" and outside "did drivers' training".
In investigation 6 you discovered mutually exclusive events and saw that if event A was mutually exclusive from event B, then:
![]()
However, if the events A and B were not mutually exclusive, then the above relation/formula did not apply.
This focus will determine a formula for finding P(A OR B) when the events are not mutually exclusive. The demonstration below shows a Venn Diagram for two non-mutually exclusive events A and B, and provides a justification for the formula for P(A OR B).
Remember the formula P(A OR B) = P(A) + P(B) - P(A AND B) was derived based on non-mutually exclusive events. However, if the events are mutually exclusive, then P(A AND B) = 0 and the formula reduces to ![]() .
.
Although it is nice to know how the formula for finding P(A OR B) for non-mutually exclusive events can be justified or proven, that is not the main outcome of this lesson. Our main outcome is to be able to identify when events are not mutually exclusive and use the above formula to calculate P(A OR B).
Example 3
In a survey of 120 high school students it was found that 60 had a part time job, 40 were involved in clubs or other activities outside school, and 20 had both a job and were involved in clubs or other activities outside school. What is the probability that a student selected at random from the 120 has a job or is involved in clubs or other activities outside school.
Solution
Let event A be "have a part time job" and event B be "involved in clubs". Then:
![]()
![]()
![]()
Since the events are not mutually exclusive (some students are in both sets), we can use the formula developed on the previous page:
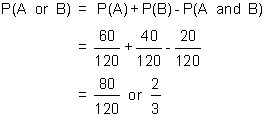
We can also represent the same problem using a Venn Diagram as shown below:
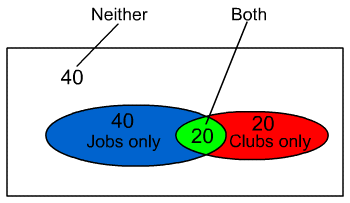
From the diagram we have:
![]()
Activity
Investigation 5 Questions p.312. Complete 21, 22, 23 and 24
Investigation 6 Questions p.313 - 314. Complete 25, 26, 27, 28 and 29
Focus Questions p.314. Complete 30 and 31
Check Your Understanding p.314 - 315. Complete 32 to 36 inclusive
When you have completed these questions, ask your on-site teacher to get the solutions for you from the Teacher's Resource Binder and check them against your answers. After you do this, if there is something you had trouble with and still do not understand, contact your on-line teacher for help.
After you do the assigned activities, continue on to the Test Yourself section below for a quick quiz on this lesson.
Test Yourself
- Out of the 120 Level 3 students in a certain high school, 40 do physics, 30 do chemistry, and 12 do both. What is the probability that if a student is selected at random from the school, they will be doing either physics or chemistry? What is the probability they will be doing neither physics nor chemistry. Are the events "doing physics" and "doing chemistry" mutually exclusive?
- The probability of having snow on the May 24th. weekend is estimated to be 45%. The probability of having snow on the November 11th. weekend is estimated to be 60%. The probability of having snow on both weekends is 15%. What is the probability of having snow on at least one of these weekends?
Click here for suggested solutions.